Bestimmung und Abhängigkeiten

Die SCHR¨ODINGER-Gleichung, deren Lösungen, die Wellenfunktionen , die Eigenschaften eines quantenmechanischen Systems beschreiben, also die Eigenschaften der Teilchenzustände zu berechnen gestatten, ist eine partielle Differentialgleichung mit Ableitungen der Wellenfunktion 2. Ordnung für die Raumkoordinaten und 1. Ordnung für die Zeitkoordinate:

Hierbei sind der LAPLACE-Operator, 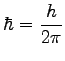die reduzierte PLANCKsche Konstante, i die imaginäre Einheit und der Nablaoperator. Zwischen dem Impuls p des betrachteten Teilchens mit der Masse m und seiner Materiewellenlänge besteht die Beziehung .