Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Partielle Differentialgleichungen Schrödinger-Gleichung Begriff der Schrödinger-Gleichung
Differentialgleichungen Partielle Differentialgleichungen Schrödinger-Gleichung Begriff der Schrödinger-Gleichung
Wenn das Potential U und die Wellenfunktion ![]() nicht von der Zeit abhängen, d.h.
nicht von der Zeit abhängen, d.h. ![]() ,
, ![]() , dann genügt zur Beschreibung der Zustände die einfachere zeitunabhängige SCHR¨ODINGER-Gleichung. Man kann sie aus der zeitabhängigen SCHR¨ODINGER-Gleichung (9.118a) mit dem Ansatz (9.2) herleiten und erhält
, dann genügt zur Beschreibung der Zustände die einfachere zeitunabhängige SCHR¨ODINGER-Gleichung. Man kann sie aus der zeitabhängigen SCHR¨ODINGER-Gleichung (9.118a) mit dem Ansatz (9.2) herleiten und erhält
 |
(9.120a) |
In diesem ebenfalls nichtrelativistischen Fall ist
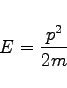 |
(9.120b) |
die Energie des Teilchens. Die Wellenfunktionen ![]() , die diese Differentialgleichung erfüllen, sind ihre Eigenfunktionen; sie existieren nur für bestimmte Energieeigenwerte
, die diese Differentialgleichung erfüllen, sind ihre Eigenfunktionen; sie existieren nur für bestimmte Energieeigenwerte ![]() , die sich für das betrachtete Problem aus seinen spezifischen Anfangs- und Randbedingungen ergeben. Die Gesamtheit der Eigenwerte bildet das Energiespektrum der Teilchen. Wenn U eine monotone Funktion ist, die im Unendlichen verschwindet, dann bilden die Eigenwerte ein diskretes Spektrum.
, die sich für das betrachtete Problem aus seinen spezifischen Anfangs- und Randbedingungen ergeben. Die Gesamtheit der Eigenwerte bildet das Energiespektrum der Teilchen. Wenn U eine monotone Funktion ist, die im Unendlichen verschwindet, dann bilden die Eigenwerte ein diskretes Spektrum.
Ist das betrachtete Gebiet der gesamte Raum, dann kann als Randbedingung gefordert werden, daß ![]() im LEBESGUEschen Sinne (s. auch [8.9]) im gesamten Raum quadratisch integrabel sein muß. Ist das Gebiet endlich, z.B. eine Kugel oder ein Zylinder, dann kann als erste Randwertaufgabe z.B.
im LEBESGUEschen Sinne (s. auch [8.9]) im gesamten Raum quadratisch integrabel sein muß. Ist das Gebiet endlich, z.B. eine Kugel oder ein Zylinder, dann kann als erste Randwertaufgabe z.B. ![]() für den Rand gefordert werden.
für den Rand gefordert werden.
In dem speziellen Fall U(x) = 0 ergibt sich die HELMHOLTZsche Differentialgleichung
mit dem Eigenwert
 |
(9.121b) |
Als Randbedingung wird hier oft ![]() am Rande gefordert. In einem endlichen Gebiet stellt (9.121a) die mathematische Ausgangsgleichung für akustische Schwingungen in gegebenen räumlichen Begrenzungen dar.
am Rande gefordert. In einem endlichen Gebiet stellt (9.121a) die mathematische Ausgangsgleichung für akustische Schwingungen in gegebenen räumlichen Begrenzungen dar.