Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Partielle Differentialgleichungen Schrödinger-Gleichung Begriff der Schrödinger-Gleichung
Differentialgleichungen Partielle Differentialgleichungen Schrödinger-Gleichung Begriff der Schrödinger-Gleichung
Den allgemeinen nichtrelativistischen Fall eines spinlosen Teilchens mit der Masse m und der Geschwindigkeit v im orts- und zeitabhängigen Potentialfeld U(x1,x2,x3,t) beschreibt die zeitabhängige SCHR¨ODINGER-Gleichung (9.118a). Die unter Besonderheiten aufgeführten speziellen Bedingungen, denen die Wellenfunktion genügen muß, lauten:
Gemäß Normierungsbedingung muß die Wahrscheinlichkeit, das Teilchen im betrachteten Gebiet zu finden, gleich 1 sein. Dazu reicht (9.119a) aus, weil das Integral stets durch einen Faktor vor ![]() auf 1 gebracht werden kann.
auf 1 gebracht werden kann.
Eine Lösung der zeitabhängigen SCHR¨ODINGER-Gleichung hat die Form
Der Zustand des Teilchens wird in einem Zeitpunkt t durch eine periodische Funktion von der Zeit mit der Kreisfrequenz ![]() beschrieben. Wenn die Energie des Teilchens in dem Zustand den festen Wert
beschrieben. Wenn die Energie des Teilchens in dem Zustand den festen Wert ![]() besitzt, dann hängt die Wahrscheinlichkeit
besitzt, dann hängt die Wahrscheinlichkeit ![]() , es in einem Raumelement dV zu finden, nicht von der Zeit ab:
, es in einem Raumelement dV zu finden, nicht von der Zeit ab:
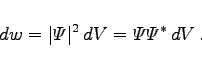 |
(9.119c) |
Man spricht vom stationären Zustand des Teilchens.