Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen 1. Ordnung Wichtige Integrationsmethoden
Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen 1. Ordnung Wichtige Integrationsmethoden
Integrierender Faktor wird eine Funktion ![]() genannt, wenn die Gleichung
genannt, wenn die Gleichung
| Mdx+Ndy=0 | (9.10a) |
durch Multiplikation mit ![]() in eine exakte Differentialgleichung übergeht. Der integrierende Faktor genügt der Differentialgleichung
in eine exakte Differentialgleichung übergeht. Der integrierende Faktor genügt der Differentialgleichung
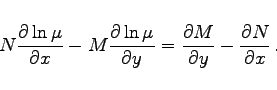 |
(9.10b) |
Jede beliebige partikuläre Lösung dieser Gleichung ist ein integrierender Faktor. In vielen Fällen ist der integrierende Faktor ![]() von der speziellen Form
von der speziellen Form ![]() oder
oder ![]() .
.
| Beispiel |
|
Es ist die Differentialgleichung (x2+y)dx-xdy =0 zu lösen. Die Gleichung für den integrierenden Faktor lautet |