Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Partielle Differentialgleichungen Schrödinger-Gleichung Teilchenbewegung im radialsymmetrischen Zentralfeld
Differentialgleichungen Partielle Differentialgleichungen Schrödinger-Gleichung Teilchenbewegung im radialsymmetrischen Zentralfeld
Die Radialgleichung (9.143d) enthält neben dem Potential V(r) noch die Separationskonstante ![]() . Man schreibt deshalb R(r) = Rl(r) und substituiert
. Man schreibt deshalb R(r) = Rl(r) und substituiert
 |
(9.144a) |
weil das Quadrat der Funktion u(r) die letztlich gesuchte Aufenthaltswahrscheinlichkeit |u(r)|2dr = |Rl(r)|2r2dr des Teilchens in einer Kugelschale zwischen r und r + dr angibt. Die Substitution führt auf die eindimensionale SCHR¨ODINGER-Gleichung
Diese enthält das effektive Potential
 |
(9.144c) |
das aus zwei Anteilen besteht. Die Rotationsenergie
 |
(9.144d) |
wird Zentrifugalpotential genannt.
Die physikalische Bedeutung von l als Bahndrehimpuls-Quantenzahl ergibt sich aus der Analogiebetrachtung zur klassischen Rotationsenergie
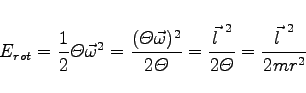 |
(9.144e) |
eines rotierenden Teilchens mit dem Trägheitsmoment ![]() und dem Bahndrehimpuls
und dem Bahndrehimpuls ![]() :
:
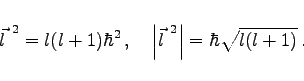 |
(9.144f) |