Begriff des Solitons

Solitonen - man spricht auch von solitären Wellen - sind physikalisch betrachtet impuls- oder auch stufenförmig lokalisierte Störungen eines nichtlinearen Mediums oder Feldes; die betreffende Energie ist auf ein enges Gebiet konzentriert. Sie treten auf:

• in Festkörpern, z.B. in anharmonischen Gittern, in JOSEPHSON-Kontakten, in Glasfasern (optische Solitonen), bei der Wanderung von BLOCH-Wänden und in quasi-eindimensionalen Leitern (PEIERLS-Phasenübergnge),
• in Flüssigkeiten als Oberflächenwellen (hohe Flutwellen in Flußmündungen, Tsunamis, d.h. seismische Wasserwellen) (s. [9.60]) oder Spinwellen,
• bei Wüstendünen als Barchane,
• in Plasmen als LANGMUIR-Solitonen,
• in linearen Molekülen (Proteinketten, z.B. -Helix als DAWYDOW-Soliton),
• in der klassischen und Quantenfeldtheorie.

Solitonen haben sowohl Teilchen- als auch Welleneigenschaften; sie sind zu jedem Zeitpunkt örtlich lokalisiert, und der Bereich der Lokalisierung, bzw. der Punkt, um den herum die Welle lokalisiert ist, bewegt sich wie ein freies Teilchen; insbesondere kann er auch ruhen. Ein Soliton besitzt eine permanente Ausbreitungsstruktur: Auf Grund einer Balance zwischen Nichtlinearität und Dispersion ändern sich Form und Geschwindigkeit nicht. Amplitude und Geschwindigkeit sind gekoppelt; ihrer Form nach unterscheidet man glockenförmige und stufenförmige Solitonen.

Mathematisch betrachtet, sind Solitonen spezielle Lösungen bestimmter nichtlinearer partieller Differentialgleichungen, die in Physik, Technik und angewandter Mathematik auftreten. Ihre Besonderheiten bestehen darin, daß sie konservativ sind (es fehlt jegliche Dissipation) sowie vollständig integrabel. Die nichtlinearen Terme können nicht störungstheoretisch behandelt werden. Eine Lösungsmethode ist die Spektraltransformation.

In nicht konservativen Systemen gibt es solitäre Wellenerscheinungen (dissipative Solitonen).

Wichtige Beispiele für Gleichungen mit Solitonenlösungen sind:

Mit x bzw. t als Index werden partielle Ableitungen bezeichnet, z.B. 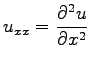. In diesen Gleichungen wird der eindimensionale Fall betrachtet, d.h., es gilt u =u(x,t), wobei x die Ortskoordinate und t die Zeit repräsentieren. Die Gleichungen sind in skalierter Form angegeben, d.h., die beiden unabhängigen Variablen x und t sind hier dimensionslose Größen. Bei praktischen Anwendungen sind sie mit den für das jeweilige Problem charakteristischen, dimensionsbehafteten Größen (Länge und Zeit) zu multiplizieren. Analoges gilt für die Geschwindigkeit v.