Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen 1. Ordnung Wichtige Integrationsmethoden
Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen 1. Ordnung Wichtige Integrationsmethoden
RICCATIsche Differentialgleichung heißt die Gleichung
die im allgemeinen nicht durch Quadraturen gelöst werden kann, d.h. nicht durch endlich viele aufeinander folgende Integrationen. Ist aber eine partikuläre Lösung y1 der RICCATIschen Differentialgleichung bekannt, dann läßt sich diese durch die Substitution
 |
(9.13b) |
auf eine lineare Differentialgleichung für z zurückführen. Kennt man noch eine zweite Lösung ![]() , so ist
, so ist
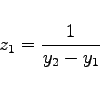 |
(9.13c) |
eine partikuläre Lösung der linearen Differentialgleichung für die Funktion ![]() , so daß sich ihre Integration vereinfacht. Sollten sogar drei Lösungen
, so daß sich ihre Integration vereinfacht. Sollten sogar drei Lösungen ![]() und y3 bekannt sein, dann lautet das allgemeine Integral der RICCATIschen Differentialgleichung
und y3 bekannt sein, dann lautet das allgemeine Integral der RICCATIschen Differentialgleichung
 |
(9.13d) |
Durch die Substitution
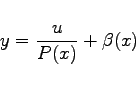 |
(9.13e) |
läßt sich die RICCATIsche Differentialgleichung stets in die Normalform
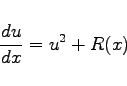 |
(9.13f) |
überführen. Mit der Substitution
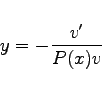 |
(9.13g) |
ergibt sich aus (9.13a) eine lineare Differentialgleichung 2. Ordnung
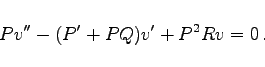 |
(9.13h) |
| Beispiel |
|
Es ist die Differentialgleichung Somit ergibt sich Man sucht partikuläre Lösungen der Form Die Substitution Durch Einsetzen der partikulären Lösung
|