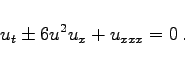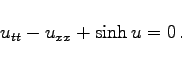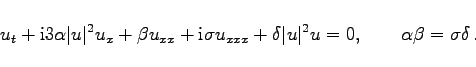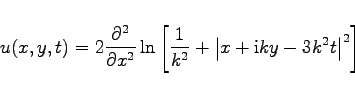Weitere nichtlineare Evolutionsgleichungen mit Solitonlösungen

Modifizierte KdV-Gleichung

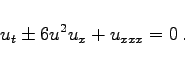(9.178)

Die noch allgemeinere Gleichung

u_t+u^pu_x+u_xxx=0

(9.179)

hat das Soliton

(9.180)

als Lösung.

sinh-GORDON-Gleichung

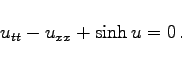(9.181)

BOUSSINESQ-Gleichung

(9.182)

Sie tritt bei der Beschreibung nichtlinearer elektrischer Netzwerke als Kontinuumsnäherung der Ladungs-Spannungs-Beziehung auf.

HIROTA-Gleichung

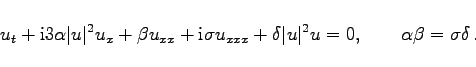(9.183)

BURGERS-Gleichung

(9.184)

Sie tritt bei der modellmäßigen Beschreibung der Turbulenz auf. Mit der HOPF-COLE-Transformation wird sie in die Diffusionsgleichung, also eine lineare Differentialgleichung, überführt.

KADOMZEV-PEDVIASHWILI-Gleichung

Die Gleichung

(u_t+6uu_x+u_xxx)_x=u_yy

(9.185a)

hat das Soliton

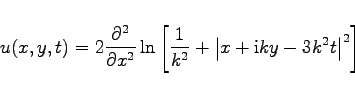(9.185b)

zur Lösung. Die Gleichung (9.185a) ist ein Beispiel für Solitonengleichungen mit einer größeren Zahl unabhängiger Variabler, z.B. zweier Ortsvariabler.