Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Partielle Differentialgleichungen Nichtlineare partielle Differentialgleichungen: Solitonen, periodische Muster und Chaos Sinus-Gordon-Gleichung
Differentialgleichungen Partielle Differentialgleichungen Nichtlineare partielle Differentialgleichungen: Solitonen, periodische Muster und Chaos Sinus-Gordon-Gleichung
Die SG-Gleichung für die Evolutionsfunktion u lautet
Sie besitzt die folgenden Solitonlösungen:
wobei  und -1<v<+1 gilt.
und -1<v<+1 gilt.
In der Abbildung ist das Kink-Soliton (9.169) der Gleichung (9.168) für v=1/2 dargestellt.
Das Kink-Soliton ist durch die zwei dimensionslosen Parameter v und x0 bestimmt, die Geschwindigkeit ist unabhängig von der Amplitude, die Zeit- und die Ortsableitung sind gewöhnliche lokalisierte Solitonen:
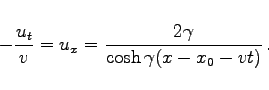 |
(9.170) |
Mit v=0 entsteht aus (9.169) bzw. (9.171) ein statisches Kink-Antikink-Soliton:
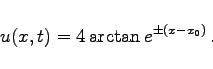 |
(9.172) |
Weitere Lösungen von (9.168) sind:
 |
(9.173) |
 |
(9.174) |
Diese Gleichung (9.175) stellt eine stationäre Welle dar, deren Einhüllende mit der Frequenz ![]() moduliert ist.
moduliert ist.
 |
(9.176a) |
Zwischen Wellenlänge ![]() und Gitterkonstante k besteht die Beziehung
und Gitterkonstante k besteht die Beziehung
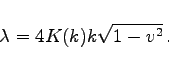 |
(9.176b) |
Für ![]() und damit
und damit ![]() , also
, also ![]() ergibt sich
ergibt sich
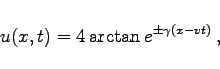 |
(9.176c) |
d.h. wieder das Kink-Soliton (9.169) und das Antikink-Soliton (9.171) mit ![]() .
.
Hinweis: Mit snx ist eine JACOBIsche elliptische Funktion mit dem Modul k und der Periode K bezeichnet:
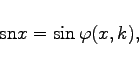 |
(9.177a) |
 |
(9.177c) |
Die Gleichung (9.177b) geht aus der inversen Funktion (14.102b) zum elliptischen Integral 1. Gattung durch die Substitution ![]() hervor.
hervor.
Die Reihenentwicklung des vollständigen elliptischen Integrals ist als Gleichung (8.104) angegeben.