Lösungen der homogenen Differentialgleichung mit konstanten Koeffizienten

Das Aufsuchen der allgemeinen Lösung der homogenen Differentialgleichung (9.40a) mit , d.h.

P_n(D)y = 0 (9.41a)

erfordert die Bestimmung der Wurzeln der sogenannten charakteristischen Gleichung

Jede Wurzel r_i liefert eine Lösung e^r_ix der Gleichung . Tritt eine Wurzel r_i mit der Vielfachheit k auf, dann sind ebenfalls Lösungen. Die Linearkombination dieser aller Lösungen ergibt die allgemeine Lösung der homogenen Differentialgleichung:

Wenn die Koeffizienten a_i reell sind, können komplexe Wurzeln der charakteristischen Gleichung nur paarweise konjugiert komplex auftreten. In diesem Falle sind z.B. für und in den betreffenden Gliedern der allgemeinen Lösungen die Funktionen e^r₁x und e^r₂x durch und zu ersetzen. Die dabei entstehenden Ausdrücke der Form können auch in der Form mit den Konstanten A und dargestellt werden.

Beispiel

Zur Differentialgleichung y⁽⁶⁾+y⁽⁴⁾-y''-y=0 gehört die charakteristische Gleichung r⁶+r⁴-r²-1=0 mit den Wurzeln 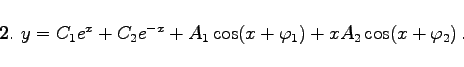. Die allgemeine Lösung kann in zwei Formen angegeben werden: