Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen höherer Ordnung und Systeme von Differentialgleichungen Lösung linearer Differentialgleichungen mit konstanten Koeffizienten
Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen höherer Ordnung und Systeme von Differentialgleichungen Lösung linearer Differentialgleichungen mit konstanten Koeffizienten
Lösungen der inhomogenen Differentialgleichung mit konstanten Koeffizienten können durch Variation der Konstanten, mit der Methode von CAUCHY oder mit Hilfe der Operatorenmethode ermittelt werden. Eine partikuläre Lösung kann sehr schnell gefunden werden, wenn die rechte Seite von (9.12) eine spezielle Form hat.
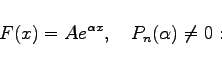 |
(9.43a) |
Eine partikuläre Lösung ist
 |
(9.43b) |
Wenn ![]() eine m-fache Wurzel der charakteristischen Gleichung ist, d.h. wenn gilt
eine m-fache Wurzel der charakteristischen Gleichung ist, d.h. wenn gilt
 |
(9.43c) |
dann ist 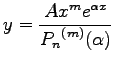 eine partikuläre Lösung. Diese Formeln können durch Anwendung des Zerlegungssatzes auch verwendet werden, wenn
eine partikuläre Lösung. Diese Formeln können durch Anwendung des Zerlegungssatzes auch verwendet werden, wenn
 |
(9.43d) |
ist. Die zugehörigen partikulären Lösungen ergeben sich als Real- bzw. Imaginärteil der Lösung derselben Differentialgleichung für
 |
(9.43e) |
auf der rechten Seite.
| Beispiel A |
|
Für die Differentialgleichung y''-6y'+8y=e2x ergeben sich die Polynome P(D) =D2-6D+8 mit P(2) =0 und P'(D) =2D-6 mit |
| Beispiel B |
|
Die Differentialgleichung |
![]() , Qn(x) ist ein Polynom n-ten Grades:
, Qn(x) ist ein Polynom n-ten Grades:
Eine partikuläre Lösung kann immer in der gleichen Form gefunden werden, d.h. als Ausdruck ![]() . R(x) ist ein mit xm multipliziertes Polynom n-ten Grades, wenn
. R(x) ist ein mit xm multipliziertes Polynom n-ten Grades, wenn ![]() eine m-fache Wurzel der charakteristischen Gleichung ist. Geht man von einem Lösungsansatz mit unbestimmten Koeffizienten des Polynoms R(x) aus und fordert man, daß er der gegebenen inhomogenen Differentialgleichung genügt, dann können die unbekannten Koeffizienten aus einem Satz linearer algebraischer Gleichungen bestimmt werden. Die Methode ist besonders in den Fällen F(x)=Qn(x) für
eine m-fache Wurzel der charakteristischen Gleichung ist. Geht man von einem Lösungsansatz mit unbestimmten Koeffizienten des Polynoms R(x) aus und fordert man, daß er der gegebenen inhomogenen Differentialgleichung genügt, dann können die unbekannten Koeffizienten aus einem Satz linearer algebraischer Gleichungen bestimmt werden. Die Methode ist besonders in den Fällen F(x)=Qn(x) für ![]() und
und ![]() oder
oder ![]() für
für ![]() anwendbar. Hier wird eine Lösung der Form
anwendbar. Hier wird eine Lösung der Form ![]() gesucht.
gesucht.
| Beispiel |
|
Die Wurzeln der zur Differentialgleichung |
Die EULERsche Differentialgleichung
 |
(9.44a) |
kann mit Hilfe der Substitution
| cx+d=et | (9.44b) |
| Beispiel |
|
Die Differentialgleichung x2y''-5xy'+8y=x2 ist ein Spezialfall der EULERschen Differentialgleichung für |