Eine endliche Teilmenge ![]() eines Vektorraums
eines Vektorraums ![]() heißt linear unabhängig, wenn aus
heißt linear unabhängig, wenn aus
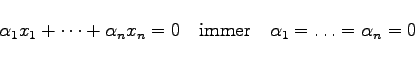 |
(12.15) |
folgt. Anderenfalls heißt sie linear abhängig. Hat man ![]() und
und ![]() beliebige Vektoren aus
beliebige Vektoren aus ![]() , dann ist aufgrund der Vektorraumaxiome
, dann ist aufgrund der Vektorraumaxiome ![]() trivialerweise das Nullelement von
trivialerweise das Nullelement von ![]() . lineare Unabhängigkeit der Vektoren
. lineare Unabhängigkeit der Vektoren ![]() bedeutet die Darstellung des Nullelements
bedeutet die Darstellung des Nullelements ![]() ausschließlich nur mit
ausschließlich nur mit ![]() . Dieser wichtige Begriff der linearen Abhängigkeit ist aus der Linearen Algebra gut bekannt und diente bereits zur Definition eines Fundamentalsystems von Lösungen für homogene Differentialgleichungen. Eine unendliche Teilmenge
. Dieser wichtige Begriff der linearen Abhängigkeit ist aus der Linearen Algebra gut bekannt und diente bereits zur Definition eines Fundamentalsystems von Lösungen für homogene Differentialgleichungen. Eine unendliche Teilmenge ![]() heißt linear unabhängig, wenn jede endliche Teilmenge von E linear unabhängig ist. Anderenfalls heißt E wieder linear abhängig.
heißt linear unabhängig, wenn jede endliche Teilmenge von E linear unabhängig ist. Anderenfalls heißt E wieder linear abhängig.
| Beispiel |
|
Bezeichnet man mit ek die Folge, deren Glieder bis auf das k-te alle gleich 0 sind und das k-te Glied gleich 1 ist, dann liegt ek im Raum 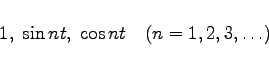 |