Inhalt Index DeskTop Bronstein
![]()
![]() Funktionalanalysis Stetige lineare Operatoren und Funktionale Lineare stetige Operatoren in Banach-Räumen
Funktionalanalysis Stetige lineare Operatoren und Funktionale Lineare stetige Operatoren in Banach-Räumen
Das soll an der folgenden Anfangswertaufgabe gezeigt werden:
| Beispiel |
|
Das Anfangswertproblem |
mit den Koeffizienten ![]() besitzt für jede rechte Seite
besitzt für jede rechte Seite ![]() und jedes Zahlenpaar
und jedes Zahlenpaar ![]() genau eine Lösung x aus
genau eine Lösung x aus ![]() , die im folgenden Sinne stetig von
, die im folgenden Sinne stetig von ![]() und
und ![]() abhängt. Sind
abhängt. Sind ![]() und gilt für
und gilt für ![]()
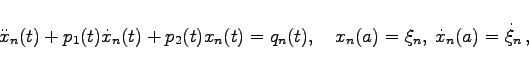 |
(12.146b) |
dann gilt:
 |
(12.146c) |