Sattelknoten-Bifurkation und transkritische Bifurkation

Gegeben sei (17.61) mit , wobei f mindestens zweimal stetig differenzierbar ist und D_xf(0,0) den Eigenwert und n-1 Eigenwerte mit Re habe.
Nach dem Satz über die Zentrumsmannigfaltigkeit werden in diesem Fall alle Bifurkationen von (17.61) nahe 0 durch eine eindimensionale reduzierte Differentialgleichung (17.63) beschrieben. Offenbar ist dabei 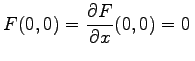. Wird zusätzlich und vorausgesetzt und die rechte Seite von (17.63) nach der TAYLOR-Formel entwickelt, so läßt sich diese Darstellung nach [17.13] durch Koordinatentransformation umformen zur Normalform

(bei ) bzw. (bei 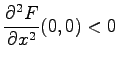), wobei eine differenzierbare Funktion mit ist und die Punkte Terme höherer Ordnung bedeuten. Für hat (17.64) nahe x = 0 zwei Ruhelagen, von denen eine stabil, die andere instabil ist. Bei verschmelzen diese zur Ruhelage , die instabil ist. Für hat (17.64) keine Ruhelage nahe 0 (s. Abbildung).

Die Übertragung auf den mehrdimensionalen Fall liefert eine Sattelknoten-Bifurkation nahe 0 in (17.61). Für n = 2 und ist diese Bifurkation in der folgenden Abbildung zu sehen.

Die Darstellung der Sattelknoten-Bifurkation im erweiterten Phasenraum ist in der nächsten Abbildung dargestellt.

Für hinreichend glatte Vektorfelder (17.61) sind Sattelknoten-Bifurkationen generisch.

Wird in den Bedingungen an F für eine Sattelknoten-Bifurkation die Voraussetzung durch die Forderungen 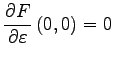und ersetzt, so ergibt sich aus (17.63) die verkürzte Normalform (ohne Glieder höherer Ordnung) einer transkritischen Bifurkation. Für n = 2 und ist die transkritische Bifurkation, zusammen mit dem Bifurkationsdiagramm, in der folgenden Abbildung gezeigt.

Sattelknoten- und transkritische Bifurkation gehören zu den Kodimension-1-Bifurkationen.