Hopf-Bifurkation

Gegeben sei (17.61) mit und . Für alle mit gelte . Die JACOBI-Matrix D_xf(0,0) habe die Eigenwerte mit und n-2 Eigenwerte mit Re. Nach dem Satz über die Zentrumsmannigfaltigkeit wird die Bifurkation durch eine zweidimensionale reduzierte Differentialgleichung (17.63) in der Form

beschrieben, wobei und g₂ differenzierbare Funktionen sind und sowie gilt. Durch eine nichtlineare Koordinatentransformation im Komplexen und Einführung von Polarkoordinaten läßt sich (17.65) auf die Normalform

bringen, in der mit Punkten die Glieder höherer Ordnung angedeutet werden. Die TAYLOR-Entwicklung der Koeffizientenfunktionen von (17.66) führt auf die verkürzte Normalform

Der Satz von ANDRONOV und HOPF garantiert, daß (17.67) die Bifurkationen von (17.66) nahe der Ruhelage bei beschreibt.

Unter der Annahme ergeben sich für (17.67) folgende Fälle:

1. a(0) <0

(Siehe Abbildung).

a) :

Stabiler Grenzzyklus und instabile Ruhelage.

b) :

Zyklus und Ruhelage verschmelzen in eine Ruhelage, die stabil wird.

c) :

Alle Orbits nahe (0,0) streben wie in b) für spiralartig gegen die Ruhelage (0,0).

2. a(0) > 0

(Siehe Abbildung).

a) :

Instabiler Grenzzyklus.

b) :

Zyklus und Ruhelage verschmelzen in eine instabile Ruhelage.

c) :

Spiralartige instabile Ruhelage wie in b).

Die Interpretation der obigen Fälle für das Ausgangssystem (17.61) zeigt die Bifurkation eines Grenzzyklus aus einer zusammengesetzten Ruhelage (zusammengesetzter Strudel der Vielfachheit 1), die HOPF-Bifurkation (oder auch ANDRONOV-HOPF-Bifurkation) genannt wird. Der Fall a(0) <0 heißt dabei superkritisch, der Fall a(0) >0 subkritisch (unter der Annahme . Für und a(0)<0 ist die Situation auf der nächsten Abbildung zu sehen.

HOPF-Bifurkationen sind generisch und gehören zu den Kodimension-1-Bifurkationen. Die angeführten Fallunterscheidungen illustrieren die Tatsache, daß eine superkritische HOPF-Bifurkation unter den oben formulierten Voraussetzungen anhand der Stabilität eines Strudels erkannt werden kann:
Die Eigenwerte und der JACOBI-Matrix der rechten Seite von (17.61) in 0 bei seien rein imaginär, und für die restlichen Eigenwerte gelte Re. Sei weiter und sei 0 ein asymptotisch stabiler Strudel für (17.61) bei . Dann findet in (17.61) bei eine superkritische HOPF-Bifurkation statt.

Beispiel

Die VAN-DER-POLsche Differentialgleichung mit dem Parameter kann als ebene Differentialgleichung

geschrieben werden. Bei geht (17.68) in die Gleichung des harmonischen Oszillators über und hat deshalb nur periodische Lösungen und eine Ruhelage, die stabil, aber nicht asymptotisch stabil ist. Mit der Transformation für geht (17.68) in die ebene Differentialgleichung

über. Für die Eigenwerte der JACOBI-Matrix in der Ruhelage (0,0) von (17.69) gilt

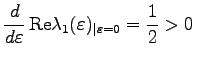und damit sowie . Wie im Beispiel gezeigt wurde, ist (0,0) eine asymptotisch stabile Ruhelage von (17.69) bei . Bei findet eine superkritische HOPF-Bifurkation statt, und (0,0) ist für kleine ein instabiler Strudel, der von einem Grenzzyklus umgeben ist, dessen Amplitude mit wächst.