Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Qualitative Theorie gewöhnlicher Differentialgleichungen Poincaré-Abbildung
Dynamische Systeme und Chaos Gewöhnliche Differentialgleichungen und Abbildungen Qualitative Theorie gewöhnlicher Differentialgleichungen Poincaré-Abbildung
Sei ![]() ein T-periodischer Orbit von (17.1) und
ein T-periodischer Orbit von (17.1) und ![]() eine (n-1)-dimensionale glatte Hyperfläche, die in x0 den Orbit
eine (n-1)-dimensionale glatte Hyperfläche, die in x0 den Orbit ![]() transversal schneidet (s. linke Abbildung).
transversal schneidet (s. linke Abbildung).
Dann gibt es eine Umgebung U von x0 und eine glatte Funktion ![]() mit
mit ![]() und
und ![]() für alle
für alle ![]() . Die Abbildung
. Die Abbildung ![]() mit
mit ![]() heißt POINCAR´E-Abbildung für
heißt POINCAR´E-Abbildung für ![]() in
in ![]() . Ist die rechte Seite f von (17.1) r-mal stetig differenzierbar, so ist P ebenfalls so oft differenzierbar. Die Eigenwerte der JACOBI-Matrix DP(x0) sind die Multiplikatoren
. Ist die rechte Seite f von (17.1) r-mal stetig differenzierbar, so ist P ebenfalls so oft differenzierbar. Die Eigenwerte der JACOBI-Matrix DP(x0) sind die Multiplikatoren ![]() des periodischen Orbits, hängen also nicht von der Wahl des x0 auf
des periodischen Orbits, hängen also nicht von der Wahl des x0 auf ![]() und der Wahl der transversalen Fläche ab. Der POINCAR´E-Abbildung kann ein System (17.3) in M =U zugeordnet werden, das erklärt ist, solange die Bildpunkte in U bleiben. Den Ruhelagen dieses zeitdiskreten Systems entsprechen periodische Orbits von (17.1), und der Stabilität dieser Ruhelagen entspricht die Stabilität der periodischen Orbits von (17.1).
und der Wahl der transversalen Fläche ab. Der POINCAR´E-Abbildung kann ein System (17.3) in M =U zugeordnet werden, das erklärt ist, solange die Bildpunkte in U bleiben. Den Ruhelagen dieses zeitdiskreten Systems entsprechen periodische Orbits von (17.1), und der Stabilität dieser Ruhelagen entspricht die Stabilität der periodischen Orbits von (17.1).
| Beispiel |
|
Für das System (17.9a) wird in Polarkoordinaten die transversale Hyperebene  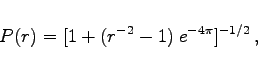 |