Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Entropien
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Entropien
Sei ![]() ein kompakter metrischer Raum und
ein kompakter metrischer Raum und ![]() ein stetiges dynamisches System mit diskreter Zeit auf
ein stetiges dynamisches System mit diskreter Zeit auf ![]() . Für beliebiges
. Für beliebiges ![]() wird eine Abstandsfunktion
wird eine Abstandsfunktion ![]() auf M durch
auf M durch
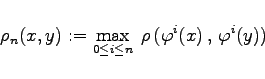 |
(17.36) |
definiert. Sei weiter ![]() die größte Anzahl von Punkten aus
die größte Anzahl von Punkten aus ![]() , die mindestens einen Abstand in der Metrik
, die mindestens einen Abstand in der Metrik ![]() von
von ![]() zueinander haben. Die topologische Entropie des zeitdiskreten dynamischen Systems (17.3) bzw. der Abbildung
zueinander haben. Die topologische Entropie des zeitdiskreten dynamischen Systems (17.3) bzw. der Abbildung ![]() ist
ist 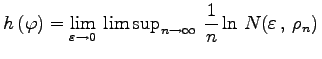 . Die topologische Entropie ist ein Maß für die Komplexität der Abbildung. Sei
. Die topologische Entropie ist ein Maß für die Komplexität der Abbildung. Sei ![]() ein weiterer kompakter metrischer Raum und
ein weiterer kompakter metrischer Raum und ![]() eine stetige Abbildung. Sind dann die beiden Abbildungen
eine stetige Abbildung. Sind dann die beiden Abbildungen ![]() und
und ![]() topologisch konjugiert, so stimmen ihre topologischen Entropien überein. Insbesondere hängt die topologische Entropie nicht von der Metrik ab. Für beliebiges
topologisch konjugiert, so stimmen ihre topologischen Entropien überein. Insbesondere hängt die topologische Entropie nicht von der Metrik ab. Für beliebiges ![]() gilt
gilt ![]() . Ist
. Ist ![]() sogar ein Homöomorphismus, so gilt
sogar ein Homöomorphismus, so gilt ![]() . Aufgrund der letzten Eigenschaft definiert man für einen Fluß
. Aufgrund der letzten Eigenschaft definiert man für einen Fluß ![]() von (17.1) auf
von (17.1) auf ![]() die topologische Entropie über
die topologische Entropie über ![]() .
.