Metrische Entropie

Sei ein dynamisches System auf mit dem Attraktor und einem auf konzentrierten invarianten Wahrscheinlichkeitsmaß . Für beliebiges seien die Würfel der Form mit , für die ist. Für beliebiges x aus einem Q_i wird der Semiorbit für wachsende t verfolgt. In Zeitabständen von werden jeweils N-mal hintereinander die Nummern der Würfel notiert, in denen sich der Semiorbit befindet. Sei die Menge aller Startwerte nahe , deren Semiorbits zu den Zeitpunkten , jeweils in liegen und sei die Wahrscheinlichkeit dafür, daß ein (typischer) Startwert in liegt. Die Entropie gibt den Zuwachs an Information an, den ein Versuch im Mittel liefert, der anzeigt, welches Ereignis aus einer endlichen Anzahl disjunkter Ereignisse wirklich eingetreten ist. In der vorliegenden Situation ist dies

wobei über alle Symbolfolgen der Länge N summiert wird, die durch Orbits in der oben beschriebenen Weise realisiert werden.

Die metrische Entropie oder KOLMOGOROV-SINAI-Entropie des Attraktors von bezüglich des invarianten Maßes ist die Größe 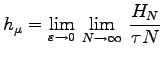. (Für zeitdiskrete Systeme entfällt der Grenzwert für .) Für die topologische Entropie von gilt . In vielen Fällen ist -invariantes Wahrscheinlichkeitsmaß auf .

Beispiel A

Sei eine stabile Ruhelage von (17.1) als Attraktor, versehen mit dem in x₀ konzentrierten natürlichen Maß . Bezüglich dieses Attraktors ist .

Beispiel B

Für die Shift- oder Modulo-Abbildung (17.28) gilt , wobei das invariante LEBESGUE-Maß sei.