Inhalt Index DeskTop Bronstein
Numerische Mathematik Numerische Integration Quadraturformeln vom Gauß-Typ
Setzt man in (19.81) als Integrationsintervall 
, und wählt man als Stützstellen die Nullstellen der LEGENDREschen Polynome (s. Tabelle LEGENDREsche Polynome), dann können die Koeffizienten 
so bestimmt werden, daß die Formel (19.81) Polynome bis zum Grad 2n+1 exakt integriert. Die Nullstellen der LEGENDREschen Polynome liegen symmetrisch zum Nullpunkt. Für die Fälle n = 1,2 und 3 erhält man:
 |
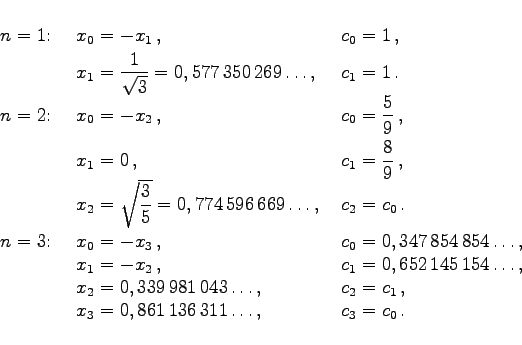(19.82) |
Hinweis: Durch die Transformation 
läßt sich das allgemeine Integrationsintervall [a,b] auf das Intervall [-1,1] transformieren. Es gilt dann: 
. Mit den obigen für das Intervall [-1,1] gültigen Werten für 
und gilt dann:
