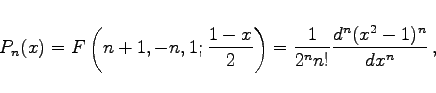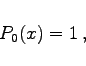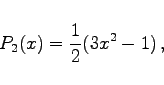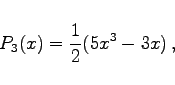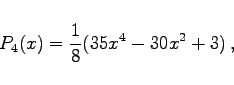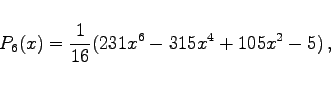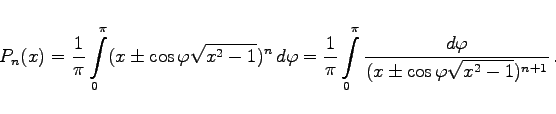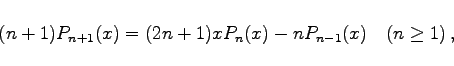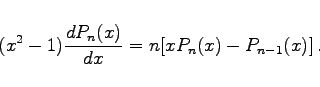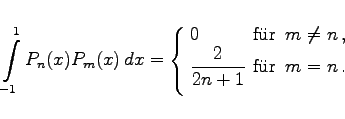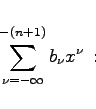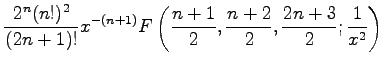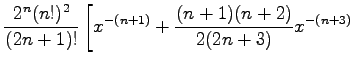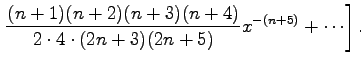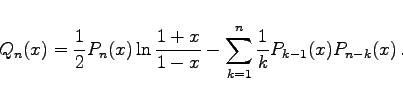Legendresche Differentialgleichung
Bei Beschränkung auf den Fall reeller Veränderlicher und ganzzahliger Parameter 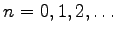 hat die LEGENDREsche Differentialgleichung die Gestalt
hat die LEGENDREsche Differentialgleichung die Gestalt
 |
(9.67a) |
Legendresche Polynome oder Kugelfunktionen 1. Art
LEGENDREsche Polynome oder Kugelfunktionen 1. Art heißen die partikulären Lösungen der LEGENDREschen Differentialgleichung für ganzzahlige  , die sich über den Potenzreihenansatz
, die sich über den Potenzreihenansatz 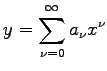 ermitteln lassen:
ermitteln lassen:
- a) Definitionsgleichung:
-
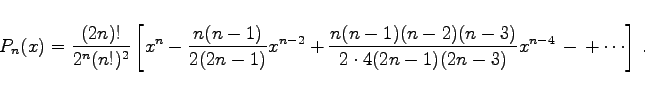 |
(9.67b) |
Dabei gilt 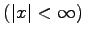 .
.
- b) Andere Darstellung:
-
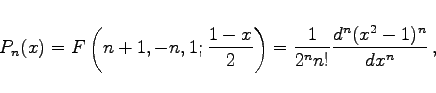 |
(9.67c) |
wobei mit F die hypergeometrische Reihe bezeichnet wird. Die ersten acht Polynome haben die folgende einfache Form:
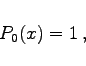 |
(9.67d) |
 |
(9.67e) |
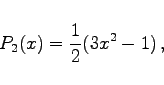 |
(9.67f) |
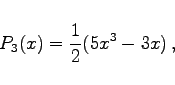 |
(9.67g) |
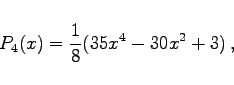 |
(9.67h) |
 |
(9.67i) |
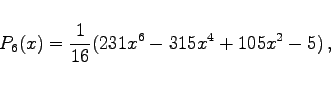 |
(9.67j) |
 |
(9.67k) |
Die Kurvenbilder von Pn(x) für Werte von n = 1 bis n = 7 sind in der folgenden Abbildung dargestellt.

Zahlenwerte können leicht mit dem Taschenrechner berechnet bzw. in der Tabelle LEGENDREsche Polynome (Kugelfunktionen) nachgesehen werden.
Eigenschaften der Legendreschen Polynome 1. Art
- a) Integraldarstellung:
-
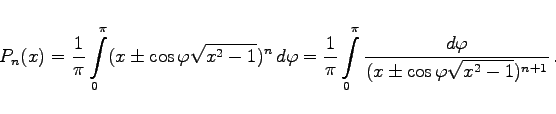 |
(9.68a) |
Das Vorzeichen kann in beiden Gleichungen beliebig genommen werden.
- b) Rekursionsformel:
-
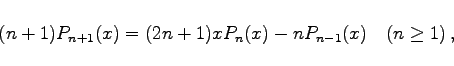 |
(9.68b) |
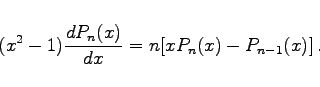 |
(9.68c) |
- c) Orthogonalitätsrelation:
-
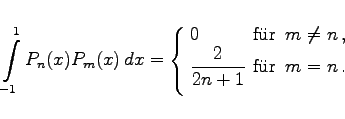 |
(9.68d) |
Zur Orthogonalität s. auch Orthogonale Systeme.
- d) Nullstellensatz:
- Alle n Nullstellen von Pn(x) sind reell und einfach und liegen im Intervall (-1,1).
- e) Erzeugende Funktion:
- Die LEGENDREschen Polynome 1. Art können auch als Reihenentwicklung der Funktion
 |
(9.68e) |
erzeugt werden.
Weitere Angaben über die LEGENDREschen Polynome 1. Art s. [21.1].
Eine zweite partikuläre, von Pn(x) linear unabhängige Lösung Qn(x) erhält man für |x| > 1 durch die Potenzreihenentwicklung
Die für |x|<1 gültige Darstellung von Qn(x) lautet:
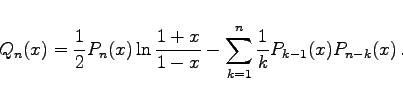 |
(9.69b) |
Man bezeichnet die Kugelfunktionen 1. und 2. Art auch als zugeordnete oder assoziierte LEGENDREsche Funktionen (s. auch Lösung der Polargleichung).
![]()
![]() Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen höherer Ordnung und Systeme von Differentialgleichungen Lineare Differentialgleichungen 2. Ordnung
Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen höherer Ordnung und Systeme von Differentialgleichungen Lineare Differentialgleichungen 2. Ordnung
![]() hat die LEGENDREsche Differentialgleichung die Gestalt
hat die LEGENDREsche Differentialgleichung die Gestalt
![]() , die sich über den Potenzreihenansatz
, die sich über den Potenzreihenansatz 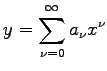 ermitteln lassen:
ermitteln lassen: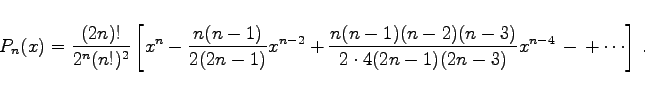
![]() .
.