Inhalt Index DeskTop Bronstein
![]()
![]() Numerische Mathematik Integration gewöhnlicher Differentialgleichungen Anfangswertaufgaben Konvergenz, Konsistenz, Stabilität
Numerische Mathematik Integration gewöhnlicher Differentialgleichungen Anfangswertaufgaben Konvergenz, Konsistenz, Stabilität
Bei vielen Anwendungen, z.B. in der chemischen Kinetik, führen mathematische Modelle auf Systeme von Differentialgleichungen, deren Lösungskomponenten sich aus verschieden stark exponentiell abklingenden Anteilen zusammensetzen. Solche Systeme von Differentialgleichungen werden als steif bezeichnet. In dem Beispiel
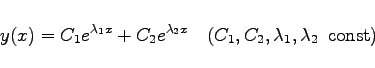 |
(19.117) |
mit ![]() und
und ![]() leistet für den Fall
leistet für den Fall ![]() der zu
der zu ![]() gehörende Term keinen Beitrag zur Lösung, er beeinflußt aber ganz wesentlich die Wahl der Schrittweite h eines Näherungsverfahrens, so daß der Einfluß der Rundungsfehler sehr stark anwächst. Dann ist die Auswahl geeigneter Näherungsverfahren unbedingt notwendig (s. [19.29], [19.6]).
gehörende Term keinen Beitrag zur Lösung, er beeinflußt aber ganz wesentlich die Wahl der Schrittweite h eines Näherungsverfahrens, so daß der Einfluß der Rundungsfehler sehr stark anwächst. Dann ist die Auswahl geeigneter Näherungsverfahren unbedingt notwendig (s. [19.29], [19.6]).