Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Vektoralgebra und analytische Geometrie Analytische Geometrie des Raumes Gleichung einer Fläche
Geometrie Vektoralgebra und analytische Geometrie Analytische Geometrie des Raumes Gleichung einer Fläche
Die Gleichung einer Rotationsfläche, d.h. einer Fläche, die durch Rotation einer gegebenen Kurve in der x,z-Ebene mit der Gleichung z = f(x) erzeugt wird, ergibt sich allgemein zu
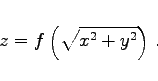 |
(3.395) |
In Analogie dazu werden die Gleichungen von Flächen erhalten, die durch Rotation einer gegebenen Kurve um eine andere Koordinate entstehen.
Die Gleichung einer Kegelfläche, deren Spitze im Koordinatenursprung liegt (s. Kegel), ist von der Gestalt ![]() wobei F eine homogene Funktion der Koordinaten ist (s. homogene Funktion).
wobei F eine homogene Funktion der Koordinaten ist (s. homogene Funktion).