Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Vektoralgebra und analytische Geometrie Analytische Geometrie des Raumes Gerade und Ebene im Raum
Geometrie Vektoralgebra und analytische Geometrie Analytische Geometrie des Raumes Gerade und Ebene im Raum
Jede in den Koordinaten lineare Gleichung definiert eine Ebene, und umgekehrt ist die Gleichung jeder Ebene vom ersten Grade.
Die allgemeine Ebenengleichung lautet
 |
(3.399b) |
wobei der Vektor ![]() senkrecht auf der Ebene steht. (In der Abbildung sind die Achsenabschnitte der Ebene a,b,c eingezeichnet.)
senkrecht auf der Ebene steht. (In der Abbildung sind die Achsenabschnitte der Ebene a,b,c eingezeichnet.)
(Zum Skalarprodukt zweier Vektoren s. Skalarprodukt und Skalarprodukt in affinen Koordinaten, zur Ebenengleichung in Vektorschreibweise s. Vektorielle Gleichungen)
Man spricht vom Normalenvektor der Ebene. Seine Richtungskosinusse sind
 |
(3.399c) |
Wenn D = 0, dann geht die Ebene durch den Koordinatenursprung, für A = 0 bzw. B = 0 oder C = 0 ist die Ebene parallel zur x-Achse, bzw. zur y- oder z-Achse. Wenn ![]() bzw. A = C = 0 oder
bzw. A = C = 0 oder ![]() dann liegt die Ebene parallel zur x,y-Ebene, bzw. zur x,z- oder y,z-Ebene.
dann liegt die Ebene parallel zur x,y-Ebene, bzw. zur x,z- oder y,z-Ebene.
Die HESSEsche Normalform der Ebenengleichung lautet
 |
(3.400b) |
wobei ![]() der Normaleneinheitsvektor der Ebene ist und p der Abstand der Ebene vom Koordinatenursprung. Die HESSEsche Normalform geht aus der allgemeinen Gleichung (3.399a) durch Multiplikation mit dem Normierungsfaktor
der Normaleneinheitsvektor der Ebene ist und p der Abstand der Ebene vom Koordinatenursprung. Die HESSEsche Normalform geht aus der allgemeinen Gleichung (3.399a) durch Multiplikation mit dem Normierungsfaktor
 |
(3.400c) |
hervor. Dabei muß das Vorzeichen von ![]() entgegengesetzt zu dem von D gewählt werden.
entgegengesetzt zu dem von D gewählt werden.
(Zum Skalarprodukt zweier Vektoren s. Skalarprodukt und Skalarprodukt in affinen Koordinaten, zur Ebenengleichung in Vektorschreibweise s. Vektorielle Gleichungen.)
Mit den Strecken ![]() die unter Berücksichtigung des Vorzeichens von der Ebene auf den Koordiantenachsen abgeschnitten werden, gilt:
die unter Berücksichtigung des Vorzeichens von der Ebene auf den Koordiantenachsen abgeschnitten werden, gilt:
 |
(3.401) |
Die Gleichung einer Ebene, die durch drei Punkte ![]() geht, lautet
geht, lautet
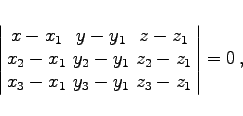 |
(3.402a) |
 |
(3.402b) |
(s. Spatprodukt dreier Vektoren).
Die Gleichung einer Ebene, die durch zwei Punkte ![]() geht und parallel zu einer Geraden mit dem Richtungsvektor
geht und parallel zu einer Geraden mit dem Richtungsvektor ![]() liegt, lautet
liegt, lautet
 |
(3.403a) |
 |
(3.403b) |
(S. auch Spatprodukt dreier Vektoren.)
Die Gleichung einer Ebene, die durch einen Punkt ![]() geht und parallel zu zwei Geraden mit den Richtungsvektoren
geht und parallel zu zwei Geraden mit den Richtungsvektoren ![]() und
und ![]() verläuft, lautet
verläuft, lautet
 |
(3.404a) |
 |
(3.404b) |
(S. auch gemischtes Produkt oder Spatprodukt dreier Vektoren.)
Die Gleichung einer Ebene, die durch einen Punkt ![]() geht und senkrecht zu einer Geraden mit dem Richtungsvektor
geht und senkrecht zu einer Geraden mit dem Richtungsvektor ![]() verläuft, lautet
verläuft, lautet
 |
(3.405a) |
 |
(3.405b) |
(Zum Skalarprodukt zweier Vektoren s. Skalarprodukt und Skalarprodukt in affinen Koordinaten.)
Einsetzen der Koordinaten des Punktes P(a,b,c) in die HESSEsche Normalform der Ebenengleichung (3.400a)
 |
(3.406a) |
liefert
 |
(3.406b) |
Wenn P und der Koordinatenursprung auf verschiedenen Seiten der Ebene liegen, ist ![]() im entgegengesetzten Falle ist
im entgegengesetzten Falle ist ![]()
Die Gleichung einer Ebene, die durch die Schnittlinie zweier Ebenen mit den Gleichungen
A1x + B1y + C1z + D1 = 0 und A2x + B2y + C2z + D2 = 0 verläuft, lautet
Dabei ist ![]() ein reeller Parameter, so daß durch die Gleichungen (3.407a) und (3.407b) ein ganzes Ebenenbüschel beschrieben wird. Die folgende Abbildung zeigt den Fall eines Ebenenbüschels mit drei Ebenen.
ein reeller Parameter, so daß durch die Gleichungen (3.407a) und (3.407b) ein ganzes Ebenenbüschel beschrieben wird. Die folgende Abbildung zeigt den Fall eines Ebenenbüschels mit drei Ebenen.
Wenn ![]() in den Gleichungen (3.407a) oder (3.407b) die Werte zwischen
in den Gleichungen (3.407a) oder (3.407b) die Werte zwischen ![]() und
und ![]() durchläuft, erhält man alle Ebenen des Büschels. Für
durchläuft, erhält man alle Ebenen des Büschels. Für ![]() erhält man die Gleichungen der Ebenen, die die Winkel zwischen den beiden gegebenen Ebenen halbieren, wenn deren Gleichungen in der Normalform gegeben sind.
erhält man die Gleichungen der Ebenen, die die Winkel zwischen den beiden gegebenen Ebenen halbieren, wenn deren Gleichungen in der Normalform gegeben sind.
(Zum Skalarprodukt zweier Vektoren s. Skalarprodukt und Skalarprodukt in affinen Koordinaten, zur Ebenengleichung in Vektorschreibweise (s. Vektorielle Gleichungen.)