Gleichungen der Elemente des begleitenden Dreibeins

1. Definition der Kurve als Schnitt zweier Flächen:

Die Definition der Kurve als Schnitt zweier Flächen erfolgt in der Form (3.540).

Dabei sind x,y,z die Koordinaten des Kurvenpunktes P und X,Y,Z die laufenden Koordinaten der Tangente bzw. der Normalebene. Die partiellen Ableitungen beziehen sich auf den Punkt P.

Tabelle Vektor- und Koordinatengleichungen von Raumkurvengrößen

Vektorgleichung	Koordinatengleichung
Tangente:
Normalebene:
	x'(X-x)+y'(Y-y)+z'(Z-z)=0
Schmiegungsebene:
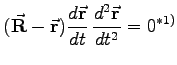Binormale:
rektifizierende Ebene:
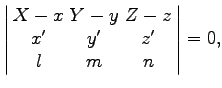	wo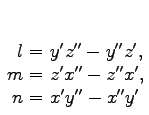
Hauptnormale:
-Ortsvektor der Raumkurve,     -Ortsvektor der Raumkurvengröße
*1) s. Spatprodukt dreier Vektoren.

Definition der Kurve als Funktion eines Parameters t in der Parameterform und als Vektorgleichung:

Die Definition der Kurve als Funktion eines Parameters t in der Parameterform und als Vektorgleichung erfolgt gemäß (3.541) und wobei (3.543).
Die Vektor- und Koordinatengleichungen von Raumkurvengrößen des Punktes P mit x,y,z sowie sind in der folgenden Tabelle zusammengefaßt. Dabei sind X,Y,Z und die laufenden Koordinaten und der Radiusvektor eines Dreibeinelements. Die Ableitungen nach dem Parameter t beziehen sich auf den Punkt .

Definition der Kurve als Funktion der Bogenlänge s in der Parameterform und als Vektorgleichung:

Die Definition der Kurve als Funktion der Bogenlänge s in der Parameterform und als Vektorgleichung erfolgt gemäß (3.542a) und wobei (3.544).
Wenn als Parameter die Bogenlänge s gewählt wird, dann gelten für die Tangente und die Binormale sowie für die Normal- und Schmiegungsebene dieselben Gleichungen wie im Falle des vorhergehenden Abschnittes; es ist lediglich t durch s zu ersetzen. Die Gleichungen der Hauptnormalen und der rektifizierenden Ebene werden einfacher, wie aus der folgenden Tabelle zu ersehen ist.

Tabelle Vektor- und Koordinatengleichungen von
Raumkurvengrößen als Funktion von der Bogenlänge

Element des Dreibeins	Vektorgleichung	Koordinatengleichung
Hauptnormale
Rektifizierende Ebene		x''(X-x)+y''(Y-y)+z''(Z-z)=0
-Ortsvektor der Raumkurve,     -Ortsvektor der Raumkurvengröße