Drehung um eine beliebige Achse
Es geht dabei um eine Drehung gegen den Uhrzeigersinn um den normierten Vektor  mit
mit  um den Winkel
um den Winkel  in 5 Teilschritten:
in 5 Teilschritten:
- 1. Rotation von
 um die y-Achse bis zur x,y-Ebene:
um die y-Achse bis zur x,y-Ebene:
 mit
mit  (4.189a).
(4.189a).
Ergebnis: Der Vektor  liegt in der x,y-Ebene.
liegt in der x,y-Ebene.- 2. Rotation von
 um die z-Achse bis zur x-Achse:
um die z-Achse bis zur x-Achse:
 mit
mit  (4.189b).
(4.189b).
Ergebnis: Der Vektor  ist parallel zur x-Achse.
ist parallel zur x-Achse.
 |
(4.189a) |
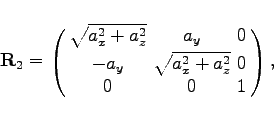 |
(4.189b) |
- 3. Rotation um den Winkel
 um die x-Achse mit
um die x-Achse mit  :
:
-
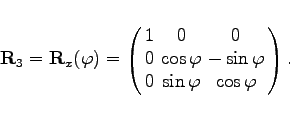 |
(4.189c) |
In den nächsten beiden Schritten werden die Rotationen  und
und  rückgängig gemacht (invertiert).
rückgängig gemacht (invertiert).
- 4. Inverse Rotation zur Rotation
 , d.h. Rotation um den Winkel
, d.h. Rotation um den Winkel 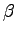
- mit
 um die z-Achse.
um die z-Achse.
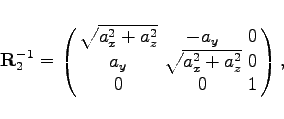 |
(4.189d) |
- 5. Inverse Rotation zur Rotation
 , d.h. Rotation um den Winkel
, d.h. Rotation um den Winkel 
- mit
 um die y-Achse.
um die y-Achse.
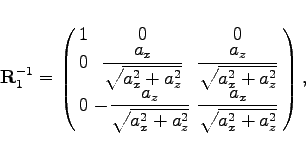 |
(4.189e) |
Damit ergibt sich als Gesamt-Matrix:
Die Matrix  ist eine orthogonale Matrix, d.h. die inverse Matrix
ist eine orthogonale Matrix, d.h. die inverse Matrix  ist gleich der transponierten Matrix.
ist gleich der transponierten Matrix.
Alternativ gilt die folgende Formel:
In dieser Formel wird der Vektor  zunächst in einen zur Achse
zunächst in einen zur Achse  parallelen Vektor
parallelen Vektor  genauer die Projektion von
genauer die Projektion von  auf
auf  und den orthogonalen Anteil
und den orthogonalen Anteil  zerlegt. Der orthogonale Anteil des Vektors liegt in der Ebene mit dem Normalenvektor
zerlegt. Der orthogonale Anteil des Vektors liegt in der Ebene mit dem Normalenvektor  und geht bei der Drehung über in
und geht bei der Drehung über in  mit dem aus
mit dem aus  durch eine (positive) Drehung um
durch eine (positive) Drehung um 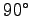 gewonnen Vektor
gewonnen Vektor 
Damit ergibt sich als Ergebnis der Drehung der Vektor
 |
(4.191) |
Vorteile
-
Standard-Darstellung in der Computergrafik,
-
kann in CARDAN-Winkel umgerechnet werden,
-
kein Gimbal Lock.
Nachteil
Für die Animation, d.h. Interpolation von Rotationen, ungeeignet.
![]()
![]() Lineare Algebra Quaternionen und Anwendungen Darstellung von Drehungen im dreidimensionalem euklidschem Raum
Lineare Algebra Quaternionen und Anwendungen Darstellung von Drehungen im dreidimensionalem euklidschem Raum
![]() mit
mit ![]() um den Winkel
um den Winkel ![]() in 5 Teilschritten:
in 5 Teilschritten:![]() und
und ![]() rückgängig gemacht (invertiert).
rückgängig gemacht (invertiert). um die y-Achse.
um die y-Achse.



 genauer die Projektion von
genauer die Projektion von 
