Inhalt Index DeskTop Bronstein
![]()
![]() Lineare Algebra Quaternionen und Anwendungen Darstellung von Drehungen im dreidimensionalem euklidschem Raum
Lineare Algebra Quaternionen und Anwendungen Darstellung von Drehungen im dreidimensionalem euklidschem Raum
Mit ![]() gilt:
gilt:
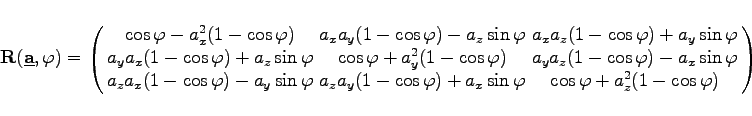 |
(4.192a) |
 |
(4.192b) |
mit  und
und 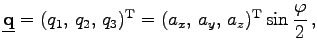 d.h. der Einheitsquaternion
d.h. der Einheitsquaternion 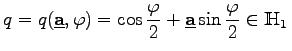 .
.
Identifiziert man ![]() so gilt
so gilt
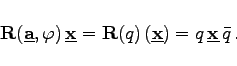 |
(4.193) |
Insbesondere ergeben sich die Spalten der Rotationsmatrix aus ![]()
 |
(4.194) |
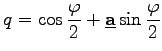 bestimmt werden.
bestimmt werden. |
(4.195) |
der inversen Rotation entspricht die konjugierte Quaternion, d.h.
 |
(4.196) |
| Beispiel Quaternionen, Rotation um phi =60 Grad um die Achse (1,1,1)T | ||||||||||||
|
Zuerst wird die Achse gemäß 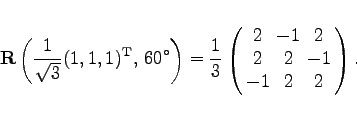 Die die Rotation beschreibende Quaternion ist  Weiterhin ist
Die beiden anderen Spalten ergeben sich analog: 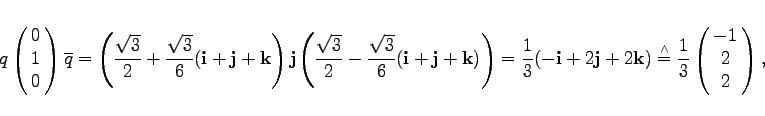   |