Inhalt Index DeskTop Bronstein
![]()
![]() Lineare Algebra Tensoren Tensoren mit speziellen Eigenschaften Invariante Tensoren
Lineare Algebra Tensoren Tensoren mit speziellen Eigenschaften Invariante Tensoren
Sind ![]() und
und ![]() die Einheitsvektoren in Richtung der Achsen eines rechtwinkligen Koordinatensystems, dann gilt für das Spatprodukt
die Einheitsvektoren in Richtung der Achsen eines rechtwinkligen Koordinatensystems, dann gilt für das Spatprodukt
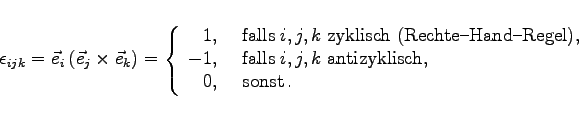 |
(4.79a) |
Das sind insgesamt 33=27 Elemente, die als Elemente eines 3stufigen Tensors aufgefaßt werden können. Im Falle einer Drehung des Koordinatensystems folgt aus dem Transformationsgesetz (4.68)
 |
(4.79b) |
d.h., die Elemente sind drehungsinvariant. Paßt man sie so in ein Koordinatensystem ein, daß sie unabhängig von der Wahl des Ursprungs, also auch translationsinvariant sind, dann bilden die Zahlen ![]() einen invarianten Tensor 3. Stufe, den sogenannten Epsilontensor.
einen invarianten Tensor 3. Stufe, den sogenannten Epsilontensor.