Ringhomomorphismus und Ringisomorphismus
- 1. Ringhomomorphismus:
- Es seien
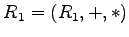 und
und 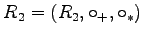 Ringe. Eine Abbildung
Ringe. Eine Abbildung  heißt Ringhomomorphismus, wenn für alle
heißt Ringhomomorphismus, wenn für alle  gilt:
gilt:
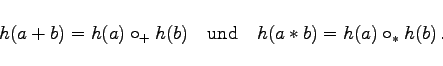 |
(5.204) |
- 2. Kern:
- Der Kern von h ist die Menge aller Elemente aus
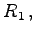 die bei h auf das neutrale Element 0 von (R2,+) abgebildet werden, und wird mit
die bei h auf das neutrale Element 0 von (R2,+) abgebildet werden, und wird mit  bezeichnet:
bezeichnet:
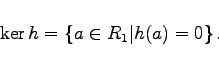 |
(5.205) |

- 3. Ringisomorphismus:
- Ist h außerdem bijektiv, so heißt h Ringisomorphismus, und die Ringe R1 und R2 heißen zueinander isomorph.
- 4. Faktorring:
- Ist I ein Ideal eines Ringes
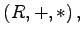 so wird die Menge der Nebenklassen
so wird die Menge der Nebenklassen  von I in der additiven Gruppe (R,+) des Ringes R bezüglich der Operationen (s. Definition und Eigenschaften von Gruppen)
von I in der additiven Gruppe (R,+) des Ringes R bezüglich der Operationen (s. Definition und Eigenschaften von Gruppen)
 |
(5.206) |
zu einem Ring, dem Faktorring von R nach I, der mit R/I bezeichnet wird.
Die Hauptideale (m) von  liefern als Faktorringe gerade die Restklassenringe
liefern als Faktorringe gerade die Restklassenringe 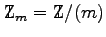
(s. Beispiele für Ringe und Körper).
![]()
![]() Algebra und Diskrete Mathematik Klassische algebraische Strukturen Ringe und Körper Homomorphismen, Isomorphismen, Homomorphiesatz
Algebra und Diskrete Mathematik Klassische algebraische Strukturen Ringe und Körper Homomorphismen, Isomorphismen, Homomorphiesatz
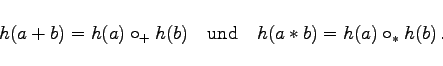
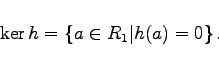
![]()

![]() liefern als Faktorringe gerade die Restklassenringe
liefern als Faktorringe gerade die Restklassenringe ![]()