Inhalt Index DeskTop Bronstein
![]()
![]() Algebra und Diskrete Mathematik Klassische algebraische Strukturen Gruppen Abbildungen zwischen Gruppen
Algebra und Diskrete Mathematik Klassische algebraische Strukturen Gruppen Abbildungen zwischen Gruppen
Die Menge der Nebenklassen eines Normalteilers N in einer Gruppe G wird bezüglich der Operation
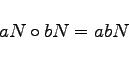 |
(5.104) |
zu einer Gruppe, der Faktorgruppe von G nach N, die mit G/N bezeichnet wird.
Der folgende Satz beschreibt einen Zusammenhang zwischen homomorphen Bildern und Faktorgruppen einer Gruppe und wird deshalb Homomorphiesatz für Gruppen genannt:
Ein Gruppenhomomorphismus ![]() bestimmt einen Normalteiler von G1, nämlich
bestimmt einen Normalteiler von G1, nämlich ![]() Die Faktorgruppe
Die Faktorgruppe ![]() ist isomorph zum homomorphen Bild
ist isomorph zum homomorphen Bild ![]() . Umgekehrt bestimmt jeder Normalteiler N von G1 eine homomorphe Abbildung
. Umgekehrt bestimmt jeder Normalteiler N von G1 eine homomorphe Abbildung ![]() mit natN (a) = aN. Diese Abbildung natN wird natürlicher Homomorphismus genannt.
mit natN (a) = aN. Diese Abbildung natN wird natürlicher Homomorphismus genannt.
| Beispiel |
|
Weil die Determinantenbildung |