Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen höherer Ordnung und Systeme von Differentialgleichungen Lineare Differentialgleichungen 2. Ordnung
Differentialgleichungen Gewöhnliche Differentialgleichungen Differentialgleichungen höherer Ordnung und Systeme von Differentialgleichungen Lineare Differentialgleichungen 2. Ordnung
Hypergeometrische Differentialgleichung heißt die Gleichung
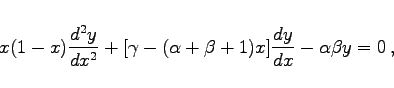 |
(9.70a) |
in der die ![]() und
und ![]() Parameter sind. Sie beinhaltet eine große Zahl wichtiger Spezialfälle.
Parameter sind. Sie beinhaltet eine große Zahl wichtiger Spezialfälle.
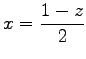 ergibt sich die LEGENDREsche Differentialgleichung.
ergibt sich die LEGENDREsche Differentialgleichung. |
(9.70c) |
 |
(9.70d) |
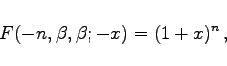 |
(9.70e) |
 |
(9.70f) |
 |
(9.70g) |
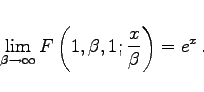 |
(9.70h) |