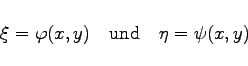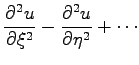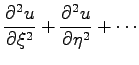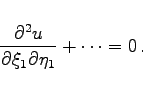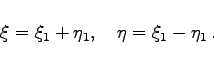Zur Transformation der Differentialgleichung (9.88a) in die Normalform der linearen partiellen Differentialgleichungen 2. Ordnung gibt es die folgenden Möglichkeiten:
- 1. Transformation in die Normalform
- Die Differentialgleichung (9.88a) kann durch die Einführung neuer unabhängiger Veränderlicher
 |
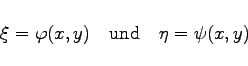(9.90a) |
in Übereinstimmung mit dem Vorzeichen der Diskriminante (9.88b) auf eine der folgenden drei Normalformen gebracht werden:
 |
= |
 |
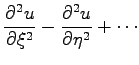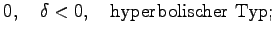(9.90b) |
 |
= |
 |
(9.90c) |
 |
= |
 |
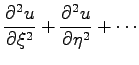(9.90d) |
Glieder, die keine partiellen Ableitungen 2. Ordnung der unbekannten Funktion enthalten, sind durch Punkte angedeutet.
- 2. Transformation in die Normalform (9.90b) beim hyperbolischen Typ
- Wenn im hyperbolischen Fall zwei Charakteristikenscharen als Koordinatenlinienscharen im neuen Koordinatensystem (9.90a) gewählt werden, d.h., wenn für die Gleichungen der Charakteristikenscharen
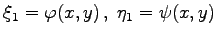mit 
gesetzt wird, dann geht (9.88a) über in
 |
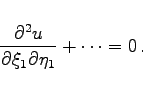(9.90e) |
Diese Form heißt ebenfalls Normalform der Differentialgleichung vom hyperbolischen Typ. Von hier gelangt man zur Normalform (9.90b) mit Hilfe der Substitution
 |
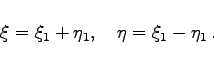(9.90f) |
- 3. Transformation in die Normalform (9.90c) beim parabolischen Typ
- Für die Schar
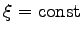wird die einzige in diesem Falle gegebene Charakteristikenschar gewählt, wobei für 
eine beliebige Funktion von x und y gewählt werden kann, die aber nicht von 
abhängen darf.
- 4. Transformation in die Normalform (9.90d) beim elliptischen Typ
- Wenn die Koeffizienten A(x,y),B(x,y),C(x,y) analytische Funktionen sind, dann definiert die Gleichung der Charakteristiken im elliptischen Falle zwei konjugiert komplexe Scharen von Kurven
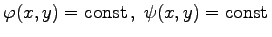. Wird 
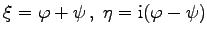gesetzt, dann geht die Gleichung in die Normalform (9.90d) über.
