Inhalt Index DeskTop Bronstein
![]()
![]() Funktionalanalysis Vektorräume Geordnete Vektorräume Kegel und Halbordnung
Funktionalanalysis Vektorräume Geordnete Vektorräume Kegel und Halbordnung
Bereits am Beispiel des mit dem ersten Quadranten als Kegel ![]() geordneten Vektorraumes
geordneten Vektorraumes ![]() wird eine typische Erscheinung in geordneten Vektorräumen ersichtlich, auf die mit den Begriffen Halbordnung oder teilweise bereits hingewiesen wurde, nämlich, daß nicht beliebige zwei Vektoren vergleichbar sein müssen. Die aus den Vektoren x=(1,-1) und y=(0,2) gebildeten Differenzen, also die Vektoren x-y=(1,-3) und
wird eine typische Erscheinung in geordneten Vektorräumen ersichtlich, auf die mit den Begriffen Halbordnung oder teilweise bereits hingewiesen wurde, nämlich, daß nicht beliebige zwei Vektoren vergleichbar sein müssen. Die aus den Vektoren x=(1,-1) und y=(0,2) gebildeten Differenzen, also die Vektoren x-y=(1,-3) und ![]() , liegen nicht in
, liegen nicht in ![]() , so daß weder
, so daß weder ![]() noch
noch ![]() gilt. Die durch einen Kegel in einem Vektorraum eingeführte Ordnung ist also lediglich eine teilweise oder partielle. Es läßt sich zeigen, daß die Relation
gilt. Die durch einen Kegel in einem Vektorraum eingeführte Ordnung ist also lediglich eine teilweise oder partielle. Es läßt sich zeigen, daß die Relation ![]() die folgenden Eigenschaften besitzt:
die folgenden Eigenschaften besitzt:
 |
(12.26) |
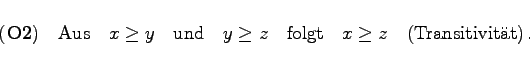 |
(12.27) |
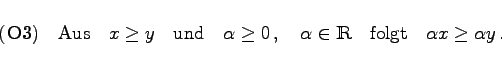 |
(12.28) |
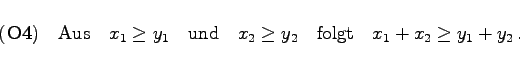 |
(12.29) |
Man nennt diese Gleichungen Axiome des geordneten Vektorraumes. Umgekehrt, ist ein Vektorraum ![]() mit einer Ordnungsrelation versehen, d.h. für gewisse Paare seiner Elemente ist eine binäre Operation
mit einer Ordnungsrelation versehen, d.h. für gewisse Paare seiner Elemente ist eine binäre Operation ![]() erklärt, die den Axiomen
erklärt, die den Axiomen ![]() bis
bis ![]() genügt, dann setzt man
genügt, dann setzt man
 |
(12.30) |
und kann zeigen, daß ![]() ein Kegel ist. Die jetzt durch
ein Kegel ist. Die jetzt durch ![]() in
in ![]() einführbare Ordnung
einführbare Ordnung ![]() ist identisch mit der vorhandenen Ordnung
ist identisch mit der vorhandenen Ordnung ![]() ; folglich sind die beiden aufgezeigten Möglichkeiten der Einführung einer Ordnung in einem Vektorraum äquivalent.
; folglich sind die beiden aufgezeigten Möglichkeiten der Einführung einer Ordnung in einem Vektorraum äquivalent.
Ein Kegel ![]() heißt erzeugend, wenn jedes Element
heißt erzeugend, wenn jedes Element ![]() als x = u-v mit
als x = u-v mit ![]() dargestellt werden kann. Man schreibt dafür auch
dargestellt werden kann. Man schreibt dafür auch ![]() -
-![]() .
.
| Beispiel A |
|
Die Ordnung im Raum |
(s. Beispiel C) eingeführt. In den Folgenräumen, betrachtet man die natürliche koordinatenweise Ordnung. Sie ergibt sich mit Hilfe des Kegels, den man in einem solchen Raum als Durchschnitt von K (s. (12.31)) mit dem jeweiligen Raum erhält. Die positiven Elemente in diesen geordneten Vektorräumen sind dann jeweils die Folgen mit nichtnegativen Gliedern. Selbstverständlich können auch andere Kegel und damit auch von der natürlichen Halbordnung verschiedene Ordnungen in diesen Räumen betrachtet werden (s. [12.20], [12.22]).
| Beispiel B |
|
In den reellen Funktionenräumen |