Bifurkation eines zweifach zusammengesetzten semistabilen periodischen Orbits

Gegeben sei das System (17.61) mit und . Das System (17.61) habe bei den periodischen Orbit mit den Multiplikatoren und .
Nach dem Satz über die Zentrumsmannigfaltigkeit für Abbildungen werden Bifurkationen in der POINCAR´E-Abbildung (17.72) durch die eindimensionale reduzierte Abbildung (17.74) mit A^c = 1 beschrieben. Wird dabei 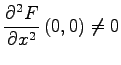und vorausgesetzt, so führt dies auf die Normalformen

(bei bzw. (bei 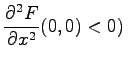. Die Iterationsverläufe von (17.75) nahe 0 und die zugehörigen Phasenporträts sind für verschiedene in den folgenden beiden Abbildungen zu sehen (s. [17.1]).

Für liegen eine stabile und eine instabile Ruhelage nahe x = 0 vor, die für in der instabilen Ruhelage x = 0 verschmelzen. Für existiert keine Ruhelage nahe . Die durch (17.75) beschriebene Bifurkation in (17.74) heißt subkritische Sattelknoten-Bifurkation für Abbildungen.

Für die Differentialgleichung (17.61) beschreiben die Eigenschaften der Abbildung (17.75) die Bifurkation eines zweifach zusammengesetzten semistabilen periodischen Orbits: Bei existieren ein stabiler periodischer Orbit und ein instabiler periodischer Orbit , die bei zu einem semistabilen Orbit verschmelzen, der sich bei auflöst (s. Abbildung).