Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Wahrscheinlichkeitsmaße auf Attraktoren Elemente der Ergodentheorie
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Wahrscheinlichkeitsmaße auf Attraktoren Elemente der Ergodentheorie
Die Aussage des Ergodensatzes ist nur dann brauchbar, wenn der Träger des Maßes ![]() möglichst groß ist. Seien
möglichst groß ist. Seien ![]() eine stetige Abbildung,
eine stetige Abbildung, ![]() ein invariantes Maß. Man sagt (s. [17.8]), daß
ein invariantes Maß. Man sagt (s. [17.8]), daß ![]() ein SBR-Maß ist (nach SINAI, BOWEN und RUELLE), wenn für jede stetige Funktion
ein SBR-Maß ist (nach SINAI, BOWEN und RUELLE), wenn für jede stetige Funktion ![]() die Menge aller der Punkte
die Menge aller der Punkte ![]() , für die
, für die
 |
(17.32a) |
gilt, ein positives LEBESGUE-Maß hat. Dafür ist ausreichend, daß die Folge der Maße
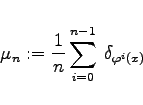 |
(17.32b) |
für fast alle ![]() schwach gegen
schwach gegen ![]() konvergiert, d.h. für jede stetige Funktion
konvergiert, d.h. für jede stetige Funktion ![]() immer
immer ![]() für
für ![]() gilt.
gilt.
| Beispiel |
|
Für einige wichtige Attraktoren, so für den HÉNON-Attraktor, wurde die Existenz eines SBR-Maßes nachgewiesen. |