Numerische Integration

Zur numerischen Integration stehen in Matlab die Prozeduren quad und quadl zur Verfügung. Beide Verfahren beruhen auf der rekursiven Anwendung von Interpolationsquadraturen mit adaptiver Gittersteuerung. Dabei basiert quad auf der SIMPSON-Formel, während in quadl LOBATTOsche Quadraturformeln höherer Ordnung verwendet werden. Daher sollte quadl bei höheren Genauigkeitsforderungen und ausreichend glatten Integranden effektiver arbeiten als quad.

Beispiel A

Als erstes Beispiel wird die näherungsweise Berechnung des bestimmten Integrals betrachtet (s. auch Beispiel Integralsinus).

Offensichtlich erkennen beide Prozeduren die (hebbare) Unstetigkeit des Integranden am linken Rand des Integrationsintervalls, können den Wert des Integrals aber trotzdem problemlos annähern. Vor dem Hintergrund der Rechnung für das Beispiel zum Rombergverfahren erscheint die Anzahl der benötigten Funktionsauswertungen hoch, ist aber in der Anlaufrechnung für die adaptive Rekursion begründet.

(Die erfolgten Warnausgaben werden nicht wiedergegeben.) Bei Vorgabe einer Genauigkeitsforderung von 10^-14, die beim Aufruf als zusätzliches Argument angegeben wird (Voreinstellung ist eine Toleranz von 10^-6), erweist sich hier die Überlegenheit von quadl.

Beispiel B

Zu berechnen ist das bestimmte Integral .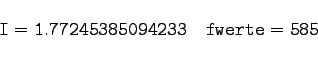

Mit dem flachen Verlauf des Integranden im sehr grossen Integrationsintervall und der relativ steilen Spitze bei x=0 kommt quad besser zurecht.