Numerische Lösung von Differentialgleichungen

Zur numerischen Lösung von Anfangswertaufgaben bei Systemen gewöhnlicher Differentialgleichungen 1. Ordnung stellt Matlab einige Verfahren bereit. Als Standardlöser dient die Prozedur ode45, in der zur Realisierung der Schrittweitensteuerung ein Paar eingebetteter RUNGE-KUTTA-Verfahren der Ordnungen 4 und 5 verwendet wird. Für höhere Genauigkeitsforderungen erweist sich das in ode113 implementierte lineare Mehrschrittverfahren vom Prediktor-Korrektor-Typ) als effektiver. Darüber hinaus gibt es Verfahren, die speziell für steife Differentialgleichungssysteme geeignet sind.

Beispiel A

Die Behandlung des Beispiels 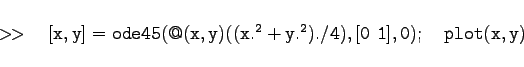zum Beispiel im Abschnitt RUNGE-KUTTA-Verfahren über dem Intervall [0,1] erfolgt durch

Der Verlauf der ermittelten Näherungslösung ist in der folgenden Abbildung dargestellt.

Beispiel B

Die numerische Lösung des Beispiels zum LORENZ-System

über dem Intervall mit den Anfangsbedingungen x(0)=(0,1,0)^T erfolgt mit dem Aufruf

Das in der folgenden Abbildung dargestellte Phasendiagramm in der x₁,x₃-Ebene wird durch das abschließende Kommando erzeugt.