Inhalt Index DeskTop Bronstein
![]()
![]() Geometrie Vektoralgebra und analytische Geometrie Analytische Geometrie der Ebene
Geometrie Vektoralgebra und analytische Geometrie Analytische Geometrie der Ebene
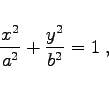 |
(3.342a) |
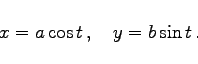 |
(3.342b) |
Die Ellipsengleichung in Polarkoordinaten ist unter Polargleichung der Kurven 2. Ordnung zu finden.
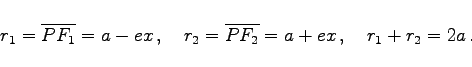 |
(3.343) |
In dieser und in den weiteren Formeln mit kartesischen Koordinaten wird angenommen, daß die Ellipse in der Normalform gegeben ist.
Jeder beliebige Ellipsenpunkt P(x,y) unterliegt der Leitlinieneigenschaft der Ellipse
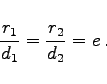 |
(3.344) |
Der geometrische Ort der Mittelpunkte aller Sehnen, die zu einem Ellipsendurchmesser parallel sind, ist wieder ein Durchmesser, ein konjugierter Durchmesser zum ersten. Für k und k' als Richtungskoeffizienten zweier konjugierter Durchmesser gilt
 |
(3.345) |
Wenn 2a1 und 2b1 die Längen zweier konjugierter Durchmesser sind und ![]() sowie
sowie ![]() die spitzen Winkel zwischen den Durchmessern und der großen Achse, wobei
die spitzen Winkel zwischen den Durchmessern und der großen Achse, wobei ![]() und
und ![]() ist, dann gilt der Satz des APOLLONIUS in der Form
ist, dann gilt der Satz des APOLLONIUS in der Form
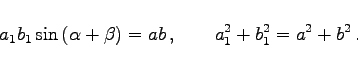 |
(3.346) |
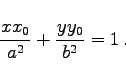 |
(3.347) |
Normale und Tangente an die Ellipse sind jeweils Winkelhalbierende des inneren Winkels und dessen Supplementwinkels zwischen den von den Brennpunkten zum Berührungspunkt P weisenden Radiusvektoren.
Die Gerade x + By + C =0 ist eine Tangente an die Ellipse, wenn die Gleichung
| A2a2 + B2b2 - C2 =0 | (3.348) |
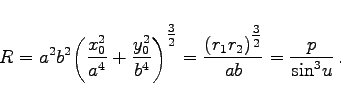 |
(3.349) |
In den Scheiteln A und B sowie C und D (rechte Abbildung) ist 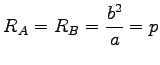 und
und 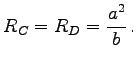
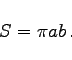 |
(3.350a) |
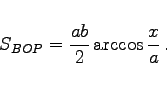 |
(3.350b) |
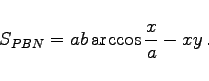 |
(3.350c) |
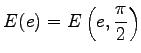 mit der numerischen Exzentrizität
mit der numerischen Exzentrizität 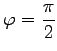 (für ein Viertel des Umfanges) zu
(für ein Viertel des Umfanges) zu
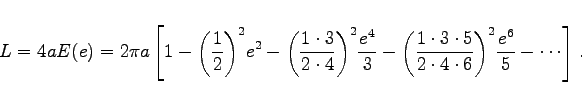 |
(3.351a) |
Setzt man 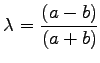 , dann ist
, dann ist
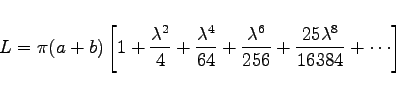 |
(3.351b) |
und in Näherung
| Beispiel |
|
Für a =1,5, b =1 liefert diese Gleichung den Wert 7,9333 für den Ellipsenbogen, während eine genauere numerische Integration mit Hilfe des vollständigen elliptischen Integrals 2. Gattung den Wert 7,932721 ergibt. Bei Anwendung der Tabelle für das vollständige elliptische Integral 2. Gattung erhält man den Näherungswert 7,94. |