Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Partielle Differentialgleichungen Schrödinger-Gleichung Linearer harmonischer Oszillator
Differentialgleichungen Partielle Differentialgleichungen Schrödinger-Gleichung Linearer harmonischer Oszillator
Gesucht ist die Aufenthaltswahrscheinlichkeit des betrachteten Teilchens in den verschiedenen Zuständen. Diese wird mit Hilfe einer physikalisch sinnvollen, d.h. normierbaren, für große Werte von y gegen Null gehenden Eigenfunktion und quadratisch integrierbaren Wellenfunktion ![]() beschrieben.
beschrieben.
Die Exponentialfunktion ![]() im Ansatz (9.151a) sorgt dafür, daß die Lösung
im Ansatz (9.151a) sorgt dafür, daß die Lösung ![]() für
für ![]() gegen Null strebt, wenn die Funktion H(y) ein Polynom ist. Daher müssen die Koeffizienten aj in (9.152a), beginnend von einem bestimmten n an, für alle j > n verschwinden:
gegen Null strebt, wenn die Funktion H(y) ein Polynom ist. Daher müssen die Koeffizienten aj in (9.152a), beginnend von einem bestimmten n an, für alle j > n verschwinden: ![]() . Mit j = n lautet die Rekursionsformel (9.152c) jetzt
. Mit j = n lautet die Rekursionsformel (9.152c) jetzt
 |
(9.153a) |
Für ![]() kann sie nur erfüllt werden, wenn
kann sie nur erfüllt werden, wenn
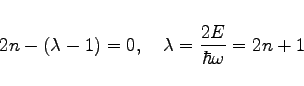 |
(9.153b) |
gesetzt wird. Somit verschwinden durch die angegebene Wahl von ![]() die Koeffizienten
die Koeffizienten ![]() . Damit auch die Koeffizienten
. Damit auch die Koeffizienten ![]() verschwinden, muß an-1 = 0 sein.
verschwinden, muß an-1 = 0 sein.
Für die spezielle Wahl ![]() erhält man die HERMITEschen Polynome der 2. Definitionsgleichung. Die ersten sechs lauten:
erhält man die HERMITEschen Polynome der 2. Definitionsgleichung. Die ersten sechs lauten:
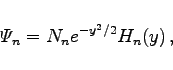 |
(9.154a) |
wobei Nn der Normierungsfaktor ist. Man erhält ihn aus der Normierungsbedingung 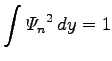 zu
zu
 |
(9.154b) |
Für die Eigenwerte der Schwingungsenergie ergibt sich als Quantisierungsbedingung aus der Bedingung für den Abbruch der Reihe mit (9.150c)
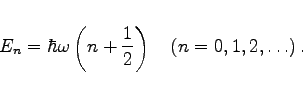 |
(9.154c) |
Das Spektrum der Energiezustände ist äquidistant. Der Summand +1/2 in der Klammer bedeutet, daß der quantenmechanische Oszillator im Unterschied zum klassischen auch im tiefsten energetischen Zustand mit n = 0 Energie besitzt, dieNullpunktsschwingungsenergie.
Die folgende Abbildung zeigt eine graphische Darstellung des äquidistanten Spektrums der Energiezustände, die zugehörigen Wellenfunktionen ![]() bis
bis ![]() sowie die Funktion der potentiellen Energie (9.149c).
sowie die Funktion der potentiellen Energie (9.149c).
Die Punkte auf der Parabel der potentiellen Energie bezeichnen die Umkehrpunkte des klassischen Oszillators, die als Amplitude  aus der Energie
aus der Energie 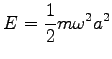 berechnet werden. Die quantenmechanische Wahrscheinlichkeit, ein Teilchen im Intervall (x, x + dx) zu finden, ist durch
berechnet werden. Die quantenmechanische Wahrscheinlichkeit, ein Teilchen im Intervall (x, x + dx) zu finden, ist durch ![]() gegeben. Sie ist auch außerhalb dieser Punkte von Null verschieden. So liefert z.B. n=1, also
gegeben. Sie ist auch außerhalb dieser Punkte von Null verschieden. So liefert z.B. n=1, also ![]() , gemäß
, gemäß  , Maxima der Aufenthaltswahrscheinlichkeit bei
, Maxima der Aufenthaltswahrscheinlichkeit bei
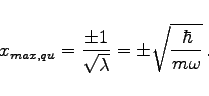 |
(9.154d) |
Für den entsprechenden klassischen Oszillator ergibt sich
 |
(9.154e) |
Die quantenmechanische Verteilungsdichte nähert sich für große Werte der Quantenzahl n in ihrem Mittelwert der klassischen.