Inhalt Index DeskTop Bronstein
![]()
![]() Differentialgleichungen Partielle Differentialgleichungen Partielle Differentialgleichungen 1. Ordnung Lineare partielle Differentialgleichungen 1. Ordnung
Differentialgleichungen Partielle Differentialgleichungen Partielle Differentialgleichungen 1. Ordnung Lineare partielle Differentialgleichungen 1. Ordnung
Die Integration der homogenen partiellen linearen Differentialgleichung ist der Integration des sogenannten charakteristischen Systems
äquivalent. Zur Lösung dieses Systems können zwei Wege eingeschlagen werden:
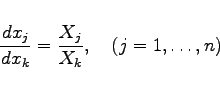 |
(9.78b) |
übergeht.
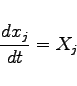 |
(9.78c) |
gesetzt wird.
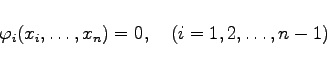 |
(9.78d) |
unabhängig sind (s. Fundamentalsystem von Lösungen), dann gilt
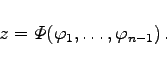 |
(9.78e) |
Dabei ist ![]() eine beliebige Funktion der n-1 Argumente
eine beliebige Funktion der n-1 Argumente ![]() und eine allgemeine Lösung der homogenen linearen Differentialgleichung von (9.77a).
und eine allgemeine Lösung der homogenen linearen Differentialgleichung von (9.77a).