Inhalt Index DeskTop Bronstein
![]()
![]() Integraltransformationen Z-Transformation Eigenschaften der Z-Transformation
Integraltransformationen Z-Transformation Eigenschaften der Z-Transformation
Die Umkehrung der Z-Transformation oder kurz Rücktransformation besteht darin, zu einer gegebenen Bildfunktion F(z) die zugehörige, eindeutige Originalfolge {fn} zu finden. Man schreibt dann
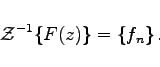 |
(15.131) |
Für die Rücktransformation gibt es verschiedene Möglichkeiten.
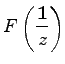
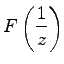 eine Reihe nach aufsteigenden Potenzen von z ist, ergibt sich wegen (15.109) nach der TAYLOR-Formel
eine Reihe nach aufsteigenden Potenzen von z ist, ergibt sich wegen (15.109) nach der TAYLOR-Formel
| Beispiel | ||||||||||||||||
|
|