Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Rekonstruktion der Dynamik aus Zeitreihen Rekonstruktionen mit prävalenten Eigenschaften
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Rekonstruktion der Dynamik aus Zeitreihen Rekonstruktionen mit prävalenten Eigenschaften
Gegeben sei ein dynamisches System ![]() mit
mit ![]() , generiert durch
, generiert durch ![]() bzw.
bzw. ![]() . In U habe
. In U habe ![]() einen Attraktor
einen Attraktor ![]() mit invariantem Wahrscheinlichkeitsmaß
mit invariantem Wahrscheinlichkeitsmaß ![]() . Es seien
. Es seien ![]() eine Meßfunktion,
eine Meßfunktion, ![]() der Ordnungsparameter,
der Ordnungsparameter, ![]() die Zeitverschiebung und für
die Zeitverschiebung und für ![]()
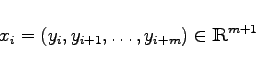 |
(17.59) |
mit ![]() eine zum Orbit
eine zum Orbit ![]() mit
mit ![]() gemessene Zeitreihe der Ordnung m +1 in vorauseilenden Koordinaten. Für Vektoren xi und xj wird ihr Abstand durch
gemessene Zeitreihe der Ordnung m +1 in vorauseilenden Koordinaten. Für Vektoren xi und xj wird ihr Abstand durch ![]() definiert. Bezeichnet N >m eine natürliche Zahl und
definiert. Bezeichnet N >m eine natürliche Zahl und ![]() eine reelle Zahl, so heißt der Ausdruck
eine reelle Zahl, so heißt der Ausdruck

| (17.60) |
 existiert, liefert diese eine Schätzung der Korrelationsdimension
existiert, liefert diese eine Schätzung der Korrelationsdimension | Beispiel |
|
Das Lorenz-System gehört zu |