Inhalt Index DeskTop Bronstein
![]()
![]() Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Lyapunov-Exponenten
Dynamische Systeme und Chaos Quantitative Beschreibung von Attraktoren Lyapunov-Exponenten
Die Formel ![]() , wobei
, wobei ![]() wieder als Halbachsenlängen eines aus der Einheitskugel mit Mittelpunkt x durch Deformation mit
wieder als Halbachsenlängen eines aus der Einheitskugel mit Mittelpunkt x durch Deformation mit ![]() hervorgegangenen Ellipsoids interpretiert werden können, kann zur Berechnung der LYAPUNOV-Exponenten benutzt werden, wenn außerdem noch Reorthonormalisierungsverfahren, wie das von HOUSHOLDER, herangezogen werden. Die Funktion
hervorgegangenen Ellipsoids interpretiert werden können, kann zur Berechnung der LYAPUNOV-Exponenten benutzt werden, wenn außerdem noch Reorthonormalisierungsverfahren, wie das von HOUSHOLDER, herangezogen werden. Die Funktion ![]() ist Lösung der zum Semiorbit
ist Lösung der zum Semiorbit ![]() des Flusses
des Flusses ![]() gehörigen Variationsgleichung mit Anfang v zur Zeit
gehörigen Variationsgleichung mit Anfang v zur Zeit ![]() . In der Tat, ist
. In der Tat, ist ![]() der Fluß von (17.1), so lautet die Variationsgleichung
der Fluß von (17.1), so lautet die Variationsgleichung ![]() . Die Lösung dieser Gleichung mit Anfang v zur Zeit t = 0 ist darstellbar als
. Die Lösung dieser Gleichung mit Anfang v zur Zeit t = 0 ist darstellbar als ![]() , wobei
, wobei ![]() die bei t = 0 normierte Fundamentalmatrix der Variationsgleichung ist, die, nach dem Satz über die Differenzierbarkeit nach den Anfangszuständen, Lösung der Matrix-Differentialgleichung
die bei t = 0 normierte Fundamentalmatrix der Variationsgleichung ist, die, nach dem Satz über die Differenzierbarkeit nach den Anfangszuständen, Lösung der Matrix-Differentialgleichung ![]() mit Anfang Z(0) = En ist.
mit Anfang Z(0) = En ist.
Die Zahl  beschreibt das Verhalten der Orbits
beschreibt das Verhalten der Orbits ![]() , mit Anfang
, mit Anfang ![]() bezüglich des Ausgangsorbits
bezüglich des Ausgangsorbits ![]() in der Richtung
in der Richtung ![]() . Ist
. Ist ![]() , so heißt dies, daß in Richtung v für wachsende t eine Annäherung der Orbits stattfindet; ist dagegen
, so heißt dies, daß in Richtung v für wachsende t eine Annäherung der Orbits stattfindet; ist dagegen ![]() , so entfernen sich die Orbits (s. Abbildung).
, so entfernen sich die Orbits (s. Abbildung).
Für die Summe aller LYAPUNOV-Exponenten von ![]() mit dem Attraktor
mit dem Attraktor ![]() und dem dort konzentrierten invarianten Maß
und dem dort konzentrierten invarianten Maß ![]() gilt für
gilt für ![]() -fast alle
-fast alle ![]() im Falle eines Flusses von (17.1)
im Falle eines Flusses von (17.1)
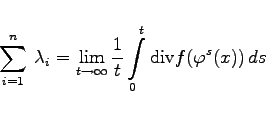 |
(17.39a) |
und für ein zeitdiskretes System (17.3)
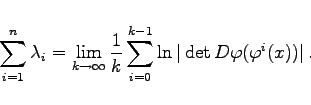 |
(17.39b) |
In dissipativen Systemen gilt also  . Dies, zusammen mit der Tatsache, daß für Flüsse einer der LYAPUNOV-Exponenten Null ist, falls der Attraktor keine Ruhelage ist, gestattet Vereinfachungen bei der Berechnung der LYAPUNOV-Exponenten (s. [17.16]).
. Dies, zusammen mit der Tatsache, daß für Flüsse einer der LYAPUNOV-Exponenten Null ist, falls der Attraktor keine Ruhelage ist, gestattet Vereinfachungen bei der Berechnung der LYAPUNOV-Exponenten (s. [17.16]).
| Beispiel A |
|
Sei x0 eine Ruhelage des Flusses von (17.1) und seien |
| Beispiel B |
|
Sei |