Inhalt Index DeskTop Bronstein
![]()
![]() Numerische Mathematik Integration gewöhnlicher Differentialgleichungen Anfangswertaufgaben Runge-Kutta-Verfahren
Numerische Mathematik Integration gewöhnlicher Differentialgleichungen Anfangswertaufgaben Runge-Kutta-Verfahren
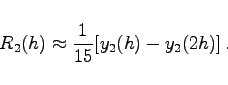 |
(19.100) |
Alternativ ist die Realisierung einer Fehlerschätzung durch die Nutzung eines Paares von RUNGE-KUTTA-Verfahren möglich, deren Ordnungen sich um 1 unterscheiden. Die beiden Verfahren sollten in ihren Zwischenstufen möglichst weitgehend übereinstimmen; man spricht dann von eingebetteten RUNGE-KUTTA-Verfahren [19.17]
Informationen über die Realisierung dieser sogenannten Schrittweitensteuerung findet man in der Literatur (s. [19.31], [19.6]).