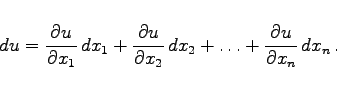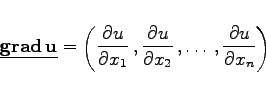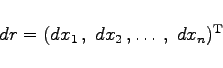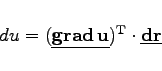Inhalt Index DeskTop Bronstein
![]()
![]() Differentialrechnung Differentiation von Funktionen von mehreren Veränderlichen Vollständiges Differential und Differentiale höherer Ordnung Begriff des vollständigen Differentials einer Funktion von mehreren Veränderlichen (totales Differential)
Differentialrechnung Differentiation von Funktionen von mehreren Veränderlichen Vollständiges Differential und Differentiale höherer Ordnung Begriff des vollständigen Differentials einer Funktion von mehreren Veränderlichen (totales Differential)